Question

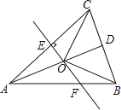
【题目】如图，△ABC中，点D在BC上，点E在AB上，BD=BE，要使△ADB≌△CEB，还需添加一个条件．

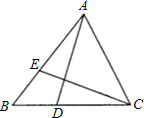
(1)给出下列四个条件：①AD=CE ②AE=CD ③∠BAC=∠BCA ④∠ADB=∠CEB请你从中选出一个能使△ADB≌△CEB的条件，并给出证明；

你选出的条件是

证明：

(2)在(1)中所给出的条件中，能使△ADB≌△CEB的还有哪些？直接在题后横线上写出满足题意的条件序号：

Answer 1

【答案】（1）详见解析；（2）③④

【解析】

要证明△ADB≌△CEB，两三角形中已知的条件有BD=BE，有一个公共角，那么根据三角形的判定公理和推论，我们可看出①不符合条件，没有SSA的判定条件，因此不正确．②AE=CD，可得出AB=BC，这样就构成了SAS，因此可得出全等的结论．③构成了全等三角形判定中的AAS，因此可得出三角形全等的结论．④构成了全等三角形判定中的ASA，因此可得出三角形全等的结论．

第（1）题添加条件②，③，④中任一个即可，以添加②为例说明．

（1）②，证明：∵AE=CD，BE=BD，∴AB=CB．

又∵∠ABD=∠CBE，BE=BD，∴△ADB≌△CEB．

（2）③构成了全等三角形判定中的AAS，因此可得出三角形全等的结论．④构成了全等三角形判定中的ASA，因此可得出三角形全等的结论．故答案为：③④．