题目内容
【题目】如图，四边形ABCD中，∠ABC=3∠CBD，∠ADC=3∠CDB，∠C=130°，则∠A的度数是（ ）
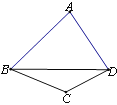
A．60° B．70° C．80° D．90°
【答案】C
【解析】
试题根据三角形的内角和定理和已知条件∠C=130°，可求得∠CBD+∠CDB的度数，再由已知条件四边形ABCD中，∠ABC=3∠CBD，∠ADC=3∠CDB，根据四边形的内角和定理，即可求得∠A的度数．
解：∵∠C+∠CBD+∠CDB=180°，∠C=130°，
∴∠CBD+∠CDB=50°，
又∵四边形ABCD中，∠ABC=3∠CBD，∠ADC=3∠CDB，
∴∠ABC+∠ADC=3（∠CBD+∠CDB）=150°，
∴∠A=360°-130°-150°=80°．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
【题目】光明中学八年级甲、乙、丙三个班中，每班的学生人数都为40名，某次数学考试的成绩统计如图：(每组分数含最小值，不含最大值)
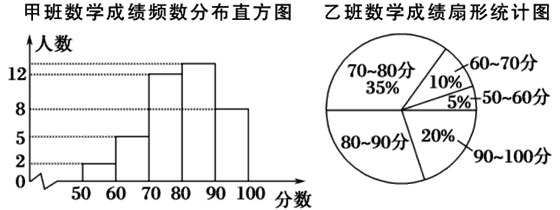
丙班数学成绩频数统计表
分数 | 50～60 | 60～70 | 70～80 | 80～90 | 90～100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息，则80～90分这一组人数最多的班是________
