Question

【题目】如图，在△ABC中，AC=2，∠BA C=75°，∠ACB= 60°，高BE与AD相交于点H,则DH的长为

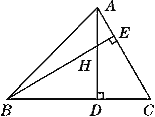
A. 2 B. 1.5 C. 1 D. 0.5

Answer 1

【答案】C

【解析】

根据∠BAC=75°，∠C=60°，得出∠BAD=45°，利用等腰直角三角形的性质和全等三角形的判定和性质得出DH=DC，再利用30°角所对直角边等于斜边的一半即可得到结论．

∵∠BAC=75°，且高BE与AE相交于H，∠C=60°，∴∠DAC=∠EBD=30°，∴∠BAD=45°，∴△BAD是等腰直角三角形，∴BD=AD．

在△BDH与△ADC中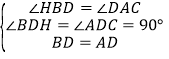，∵，∴△BDH≌△ADC（AAS），∴DH=DC．∵∠DAC=30°，∴CD=AC=1，∴DH=1.

故选C．