题目内容
【题目】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．
（初步思考）
我们不妨将问题用符号语言表示为：在△DEF中，AC＝DF，BC＝EF，∠B＝∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
（深入探究）
第一种情况：当∠B是直角时，△ABC≌△DEF．
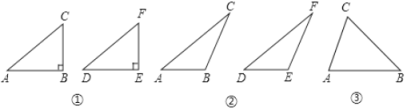
（1）如图①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根据______，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
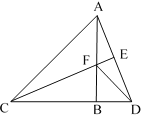
（2）如图②，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B、∠E都是钝角．求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
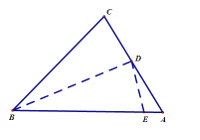
（3）在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B、∠E都是锐角．请你用直尺在图③中作出△DEF，使△DEF和△ABC不全等，并作简要说明．
【答案】（1）HL；（2）见解析；（3）如图②，见解析；△DEF就是所求作的三角形，△DEF和△ABC不全等．
【解析】
（1）根据直角三角形全等的方法“HL”证明；
（2）过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H，根据等角的补角相等求出∠CBG=∠FEH，再利用“角角边”证明△CBG和△FEH全等，根据全等三角形对应边相等可得CG=FH，再利用“HL”证明Rt△ACG和Rt△DFH全等，根据全等三角形对应角相等可得∠A=∠D，然后利用“角角边”证明△ABC和△DEF全等；
（3）以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等；
（4）根据三种情况结论，∠B不小于∠A即可．
（1）在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等运用的是HL．
（2）证明：如图①，分别过点C、F作对边AB、DE上的高CG、FH，其中G、H为垂足．
∵∠ABC、∠DEF都是钝角
∴G、H分别在AB、DE的延长线上．
∵CG⊥AG，FH⊥DH，
∴∠CGA＝∠FHD＝90°．
∵∠CBG＝180°－∠ABC，∠FEH＝∠180°－∠DEF，∠ABC＝∠DEF，
∴∠CBG＝∠FEH．
在△BCG和△EFH中，
∵∠CGB＝∠FHE，∠CBG＝∠FEH，BC＝EF，
∴△BCG≌△EFH．
∴CG＝FH．
又∵AC＝DF．∴Rt△ACG≌△DFH．
∴∠A＝∠D．
在△ABC和△DEF中，
∵∠ABC＝∠DEF，∠A＝∠D，AC＝DF，
∴△ABC≌△DEF．
（3）如图②，△DEF就是所求作的三角形，△DEF和△ABC不全等．
暑假作业暑假快乐练西安出版社系列答案
