题目内容
【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2.下面四个结论:

①BF=![]() ;
;
②∠CBF=45°;
③∠CED=30°;
④△ECD的面积为![]() ,
,
其中正确的结论有_____.(填番号)
【答案】①②④
【解析】
利用旋转的性质得CF=CB=2,∠BCF=90°,则可得△CBF为等腰直角三角形,于是可对①②进行判断;由于直线DF垂直平分AB,则FA=FB,BE=AE,于是根据等腰三角形的性质和三角形外角性质可计算出∠ECA=∠A=22.5°,然后根据三角形内角和可计算出∠CEF,从而可对③进行判断;作EH⊥BD于H,如图,根据三角形中位线性质得EH=![]() AC=
AC=![]() +1,利用旋转性质得CD=CA=2+2
+1,利用旋转性质得CD=CA=2+2![]() ,则利用三角形面积公式可计算出△ECD的面积,从而可对④进行判断.
,则利用三角形面积公式可计算出△ECD的面积,从而可对④进行判断.
∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,
∴CF=CB=2,∠BCF=90°,
∴△CBF为等腰直角三角形,
∴BF=![]() BC=2
BC=2![]() ,∠CBF=45°,所以①②正确;
,∠CBF=45°,所以①②正确;
∵直线DF垂直平分AB,
∴FA=FB,BE=AE,
∴∠A=∠ABF,
而∠BFC=∠A+∠ABF=45°,
∴∠A=22.5°,
∵CE为斜边AB上的中线,
∴EC=EA,
∴∠ECA=∠A=22.5°,
∴∠CEF=180°﹣90°﹣2×22.5°=45°,所以③错误;
作EH⊥BD于H,如图,
∵把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,
∴CD=CA=2+2![]() ,
,
∵点E为AB的中点,
∴EH=![]() AC=
AC=![]() +1,
+1,
∴△ECD的面积=![]() (
(![]() +1)(2+2
+1)(2+2![]() )=2
)=2![]() +3,所以④正确.
+3,所以④正确.
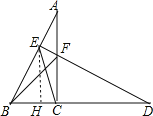
故答案为:①②④.

练习册系列答案
相关题目