题目内容
【题目】在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A、B两点,点A在点B的左侧.
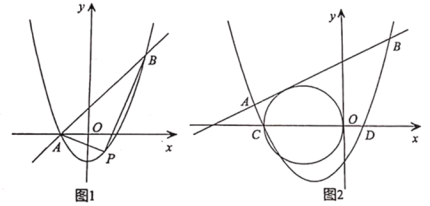
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
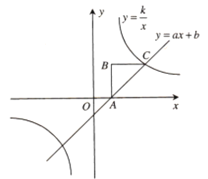
(3)如图2,抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,说明理由.
【答案】(1)A(-1,0),B(2,3);(2)△ABP面积最大值为![]() ,此时点P坐标为(
,此时点P坐标为(![]() ,﹣
,﹣![]() );(3)存在,k=
);(3)存在,k=![]() 时,使得直线y=kx+1与以OC为直径的圆相切.
时,使得直线y=kx+1与以OC为直径的圆相切.
【解析】
(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;
(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)设直线y=kx+1与以O、C为直径的圆相切的切点为Q,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与抛物线交于C点,此时不存在.
解:(1)当k=1时,抛物线解析式为y=x2-1,直线解析式为y=x+1.
联立两个解析式,得:x2-1=x+1,
解得:x=-1或x=2,
当x=-1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(-1,0),B(2,3).
(2)设P(x,x2-1),
如答图1所示,过点P作PF//y轴,交直线AB于点F,则F(x,x+1).
∴PF=yF﹣yP=(x+1)﹣(x2﹣1)=﹣x2+x+2.
S△ABP=S△PFA+S△PFB=![]() PF(xF﹣xA)+
PF(xF﹣xA)+![]() PF(xB﹣xF)=
PF(xB﹣xF)=![]() PF(xB﹣xA)=
PF(xB﹣xA)=![]() PF
PF
∴S△ABP=![]() (﹣x2+x+2)=﹣
(﹣x2+x+2)=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .当x=
.当x=![]() 时,yP=x2﹣1=﹣
时,yP=x2﹣1=﹣![]() .
.
∴△ABP面积最大值为![]() ,此时点P坐标为(
,此时点P坐标为(![]() ,﹣
,﹣![]() ).
).
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(﹣![]() ,0),F(0,1),OE=
,0),F(0,1),OE=![]() ,OF=1.
,OF=1.
在Rt△EOF中,由勾股定理得:EF=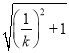 =
=![]() . 令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1. ∴C(﹣k,0),OC=k.
. 令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1. ∴C(﹣k,0),OC=k.
(Ⅰ)设直线y=kx+1与以O、C为直径的圆相切的切点为Q,如答图2所示,

则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.
设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=![]() .∴EN=OE﹣ON=
.∴EN=OE﹣ON=![]() ﹣
﹣![]() .
.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,∴△EQN∽△EOF,
∴![]() =
=![]() ,即
,即![]() =
=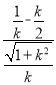 解得:k=±
解得:k=±![]() ,∵k>0,∴k=
,∵k>0,∴k=![]() .
.
∴存在实数k使得直线y=kx+1与以OC为直径的圆相切,
此时k=![]() .
.
(Ⅱ)若直线AB过点C时,此时直线与以OC为直径的圆要相切,必有AB⊥x轴,
而直线AB的解析式为y=kx+1,∴不可能相切.
综上所述,k=![]() 时,使得直线y=kx+1与以OC为直径的圆相切.
时,使得直线y=kx+1与以OC为直径的圆相切.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】2015年某省为加快建设综合交通体系,对铁路、公路、机场三个重大项目加大建设资金的投入.
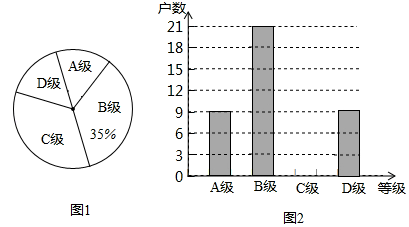
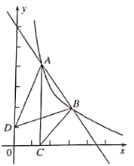
(1)机场建设项目中所有6个机场投入的建设资金金额统计如下图,已知机场![]() 投入的建设资金金额是机场
投入的建设资金金额是机场![]() 、
、![]() 所投入建设资金金额之和的三分之二,求机场
所投入建设资金金额之和的三分之二,求机场![]() 投入的建设资金金额是多少亿元?并补全条形统计图.
投入的建设资金金额是多少亿元?并补全条形统计图.
(2)将铁路、公路、机场三项建设所投入的资金金额绘制成如下扇形统计图以及统计表,根据扇形统计图及统计表中的信息,求得![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .(请直接填写计算结果)
.(请直接填写计算结果)

铁路 | 公路 | 机场 | 铁路、公路、机场三项投入建设资金总金额(亿元) | |
投入资金(亿元) | 300 |
|
|
|
所占百分比 |
| 34% | 6% | |
所占圆心角 |
|
|
|