Question

【题目】已知：正方形ABCD的边长为6，点E，F分别在边AD，边AB的延长线上，且DE=BF．

（1）如图1，连接CE，CF，EF，请判断△CEF的形状；

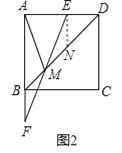
（2）如图2，连接EF交BD于M，当DE=2时，求AM的长；

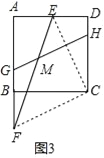
（3）如图3，点G，H分别在边AB，边CD上，且GH=3，当EF与GH的夹角为45°时，求DE的长．

Answer 1

【答案】（1）△CEF是等腰直角三角形，理由见解析；（2）；（3）3.

【解析】（1）如图1，△CEF是等腰直角三角形，理由是：

在正方形ABCD中，BC=DC，∠FBC=∠D=90°，

∵BF=DE，

∴△FBC≌△EDC，

∴CF=CE，∠ECD=∠FCB，

∴∠ECF=∠ECB+∠FCB=∠ECB+∠ECD=90°，

∴△CEF是等腰直角三角形；

（2）如图2，过E作EN∥AB，交BD于N，则EN=ED=2，

∵BN∥AD，

∴∠F=∠MEN，

∵∠BMN=∠EMN，

∴△FBM≌△ENM，

∴EM=FM，

在Rt△EAF中，EF==4，

∴AM=EF=2；

（3）如图3，连接EC和FC，

由（1）得∠EFC=45°，

∵∠EMH=45°，

∴∠EFC=∠EMH，

∴GH∥FC，

∵AF∥DC，

∴四边形FCHG是平行四边形，

∴FC=GH=3，

由勾股定理得：BF==3，

∴DE=BF=3．