题目内容
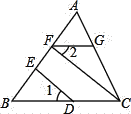
【题目】如图1,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 是
是![]() 上的点,
上的点, ![]() 相交于点
相交于点![]() .
.
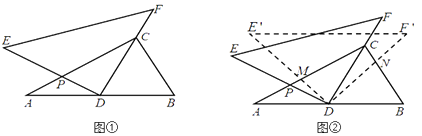
(1) 如图2,若![]() =90°,求证:
=90°,求证: ![]()
![]() ;
;
(2) 如图1,若![]() =
=![]() ( 0°<
( 0°< ![]() <180°).
<180°).
①求![]()
![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②是否存在![]() ,使
,使![]() 小于
小于![]() ,如果存在,求出
,如果存在,求出![]() 的范围,如果不存在,请说明理由.
的范围,如果不存在,请说明理由.

【答案】(1)见解析;(2) ①![]() ; ②存在,理由见解析;
; ②存在,理由见解析;
【解析】
(1) 由同角的余角相等可得![]() ,再由
,再由![]() 平分
平分![]() , 可得∠CAE=∠BAE,再由三角形的外角即可证得
, 可得∠CAE=∠BAE,再由三角形的外角即可证得![]() ;
;
(2) ①由三角形外角的性质以及角平分线的定义可得![]() ,再由三角形内角和定理即可得到
,再由三角形内角和定理即可得到![]() ;
;
②存在. 由![]() 小于
小于![]() , 可得
, 可得![]() ,继而可求得答案.
,继而可求得答案.
(1) ∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() 平分
平分![]() , ∴∠CAE=∠BAE,
, ∴∠CAE=∠BAE,
∴∠CFE=∠ACD+∠CAE,∠CEF=∠B+∠BAE,
∴![]() ;
;
(2) ①∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
②存在. ∵因为要使![]() 小于
小于![]() , 必有
, 必有![]() ,
,
即![]() , 所以
, 所以![]() ,
,
∴当![]() 时,
时,![]() 小于
小于![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目