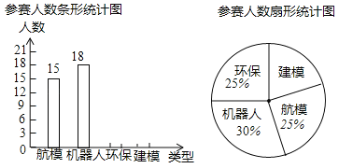
��Ŀ����
����Ŀ��������֣����������Ҷ�������ͼ1��AB��BC�ǡ�O�������ң�������ABC��Բ��һ�����ң���BC��AB��M��![]() ���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD�����������á��س�����֤��CD=AB+BD�IJ���֤�����̣�
���е㣬���M��BC�������ߵĴ���D������ABC���е㣬��CD=AB+BD�����������á��س�����֤��CD=AB+BD�IJ���֤�����̣�
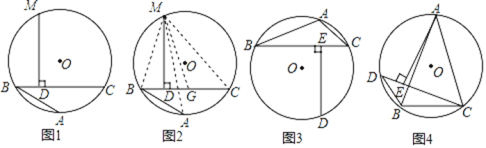
֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG
��M��![]() ���е㣬
���е㣬
��MA=MC
����
�밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
ʵ��Ӧ�ã�
��1����ͼ3����֪��ABC�ڽ��ڡ�O��BC��AB��AC��D��![]() ���е㣬���ݰ��������Ҷ����ɵ�ͼ��ij�����߶εĵ�����ϵΪBE=CE+ACBE=CE+AC��
���е㣬���ݰ��������Ҷ����ɵ�ͼ��ij�����߶εĵ�����ϵΪBE=CE+ACBE=CE+AC��
��2����ͼ4����֪������ABC�ڽ��ڡ�O��AB=AC��DΪ![]() ��һ�㣬����DB����ACD=45�㣬AE��CD�ڵ�E����BCD���ܳ�Ϊ4
��һ�㣬����DB����ACD=45�㣬AE��CD�ڵ�E����BCD���ܳ�Ϊ4![]() +2��BC=2�������AC�ij���
+2��BC=2�������AC�ij���
���𰸡�(1)������;(2)4
��������
��1������֤����MBA�ա�MGC��SAS���������ó�MB=MG�������õ��������ε����ʵó�BD=GD�����ɵó��𰸣�
��2��ֱ�Ӹ��ݰ��������Ҷ����ó����ۣ�
��3�����ݰ��������Ҷ����ó�CE=BD+DE���������CE������ù��ɶ������ɵó����ۣ�
֤������ͼ2����CB�Ͻ�ȡCG=AB������MA��MB��MC��MG��
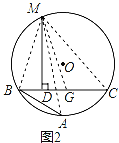
��M��![]() ���е㣬
���е㣬
��MA=MC��
����MBA����MGC��
 ��
��
���MBA�ա�MGC��SAS����
��MB=MG��
�֡�MD��BC��
��BD=GD��
��DC=GC+GD=AB+BD��
ʵ��Ӧ��
��1��BE=CE+AC��
��2�����ݰ��������Ҷ����ã�CE=BD+DE��
�ߡ�BCD���ܳ�Ϊ4![]() +2��
+2��
��BD+CD+BC=4![]() +2��
+2��
��BD+DE+CE+BC=2CE+BC=4![]() +2��
+2��
��BC=2��
��CE=2![]() ��
��
��Rt��ACE�У���ACD=45�㣬
��AC=![]() CE=4��
CE=4��