题目内容
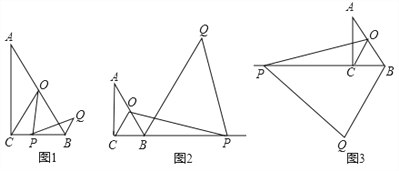
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.
【答案】(1)BQ=CP;(2)成立:PC=BQ;(3)![]() .
.
【解析】
试题(1)结论:BQ=CP.如图1中,作PH∥AB交CO于H,可得△PCH是等边三角形,只要证明△POH≌△QPB即可;
(2)成立:PC=BQ.作PH∥AB交CO的延长线于H.证明方法类似(1);
(3)如图3中,作CE⊥OP于E,在PE上取一点F,使得FP=FC,连接CF.设CE=CO=a,则FC=FP=2a,EF=![]() a,在Rt△PCE中,表示出PC,根据PC+CB=4,可得方程
a,在Rt△PCE中,表示出PC,根据PC+CB=4,可得方程![]() ,求出a即可解决问题;
,求出a即可解决问题;
试题解析:解:(1)结论:BQ=CP.
理由:如图1中,作PH∥AB交CO于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,∴CO=AO=BO,∠CBO=60°,∴△CBO是等边三角形,∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,∴∠CHP=∠CPH=60°,∴△CPH是等边三角形,∴PC=PH=CH,∴OH=PB,∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP,∵∠OPQ=∠OCP=60°,∴∠POH=∠QPB,∵PO=PQ,∴△POH≌△QPB,∴PH=QB,∴PC=BQ.
(2)成立:PC=BQ.理由:作PH∥AB交CO的延长线于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,∴CO=AO=BO,∠CBO=60°,∴△CBO是等边三角形,∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,∴∠CHP=∠CPH=60°,∴△CPH是等边三角形,∴PC=PH=CH,∴OH=PB,∵∠POH=60°+∠CPO,∠QPO=60°+∠CPQ,∴∠POH=∠QPB,∵PO=PQ,∴△POH≌△QPB,∴PH=QB,∴PC=BQ.
(3)如图3中,作CE⊥OP于E,在PE上取一点F,使得FP=FC,连接CF.
∵∠OPC=15°,∠OCB=∠OCP+∠POC,∴∠POC=45°,∴CE=EO,设CE=CO=a,则FC=FP=2a,EF=![]() a,在Rt△PCE中,PC=
a,在Rt△PCE中,PC=![]() =
=![]() =
=![]() ,∵PC+CB=4,∴
,∵PC+CB=4,∴![]() ,解得a=
,解得a=![]() ,∴PC=
,∴PC=![]() ,由(2)可知BQ=PC,∴BQ=
,由(2)可知BQ=PC,∴BQ=![]() .
.


【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?