题目内容
【题目】(1) 计算:![]()
(2) 先化简,再求值:![]() ,其中
,其中![]() 是不等式组
是不等式组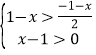 的整数解.
的整数解.
【答案】(1) 1;(2)原式=4(x1)=4.
【解析】分析:(1)先根据负整指数幂,开立方,零指数幂,特殊三角函数值进行各项运算,然后再进行加减计算即可求解,(2)先将括号里的分式进行通分进行加法计算,再进行分式除法计算,然后再解不等式组,并求出不等式组的整数解,根据分式有意义的条件,代入合适的整数解求值即可.
详解:(1)![]() ,
,
原式=4-3-1+1,
=1.
(2)![]() ,
,
原式=![]() ,
,
=![]() ,
,
=![]() ,
,
=![]() ,
,
解不等式组: ,
,
解得不等式组的解集是1<x<3,
∴不等式组的整数解为x=2.
原式=4×(21)=4.
点睛:本题主要考查实数运算和分式化简求值,解决本题的关键是要熟练掌握实数运算的相关法则和分式通分加减乘除运算法则.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 150 | 200 | 350 | 400 | 450 | 500 |
优等品的频数m | 40 | 96 | 126 | 176 | 322 | 364 | 405 | 450 |
优等品的频率 | 0.80 | 0.96 | 0.84 | 0.92 | 0.90 |
(1)填写表中的空格;
(2)画出这批乒乓球优等品频率的折线统计图;
(3)这批乒乓球优等品概率的估计值是多少?
【题目】列方程解应用题
(1)某车间有24名工人,每人毎天平均生产螺栓12个或螺母18个,两个螺栓配三个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺栓,多少名工人生产螺母?
(2)某校举行元旦汇演,七(01)、七(02)班各需购买贺卡70张,已知贺卡的价格如下:
购买贺卡数 | 不超过30张 | 30张以上不超过50张 | 50张以上 |
每张价格 | 3元 | 2.5元 | 2元 |
(i)若七(01)班分两次购买,第一次购买24张,第二次购买46张,七(02)班一次性购买贺卡70张,则七(01)班、七(02)班购买贺卡费用各是多少元?哪个班费用更节省?省多少元?
(ⅱ)若七(01)班分两次购买贺卡共70张(第二次多于第一次),共付费150元,则第一次、第二次分别购买贺卡多少张?