题目内容
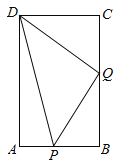
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.

(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使![]() =8cm2,试说明理由.
=8cm2,试说明理由.
【答案】(1)2秒或4秒;(2)不存在.
【解析】
试题(1)表示出PB,QB的长,利用△PBQ的面积等于8cm2列式求值即可;
(2)设出发秒x时△DPQ的面积等于8平方厘米,由三角形的面积公式列出方程,再由根的判别式判断方程是否有解即可.
试题解析:解:(1)设x秒后△PBQ的面积等于8cm2.
则AP=x,QB=2x,∴PB=6﹣x,∴![]() ×(6﹣x)2x=8,解得
×(6﹣x)2x=8,解得![]() ,
,![]() .
.
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)设出发秒x时△DPQ的面积等于8cm2.∵S矩形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ=S△DPQ,∴12×6﹣![]() ×12x﹣
×12x﹣![]() ×2x(6﹣x)﹣
×2x(6﹣x)﹣![]() ×6×(12﹣2x)=8,化简整理得:
×6×(12﹣2x)=8,化简整理得:![]() ,∵△=36﹣4×28=﹣76<0,∴原方程无解,∴不存在这样的时刻,使S△PDQ=8cm2.
,∵△=36﹣4×28=﹣76<0,∴原方程无解,∴不存在这样的时刻,使S△PDQ=8cm2.

【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
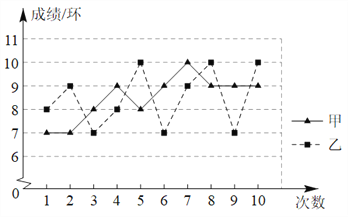
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
【题目】华联超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 25 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍:甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润多800元,求第二次乙商品是按原价打几折销售?