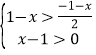题目内容
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 50 | 100 | 150 | 200 | 350 | 400 | 450 | 500 |
优等品的频数m | 40 | 96 | 126 | 176 | 322 | 364 | 405 | 450 |
优等品的频率 | 0.80 | 0.96 | 0.84 | 0.92 | 0.90 |
(1)填写表中的空格;
(2)画出这批乒乓球优等品频率的折线统计图;
(3)这批乒乓球优等品概率的估计值是多少?
【答案】(1)见解析;(2)见解析;(3)这批乒乓球优等品概率的估计值是0.90.
【解析】
(1)根据表格中数据计算填表即可;
(2)根据表格中优等品频率画折线统计图即可;
(3)利于频率估计概率求解即可.
解:(1)176÷200=0.88,364÷400=0.91,450÷500=0.90,
填表如下:
抽取的乒乓球数n | 50 | 100 | 150 | 200 | 350 | 400 | 450 | 500 |
优等品的频数m | 40 | 96 | 126 | 176 | 322 | 364 | 405 | 450 |
优等品的频率 | 0.80 | 0.96 | 0.84 | 0.88 | 0.92 | 0.91 | 0.90 | 0.90 |
(2)折线统计图如图:
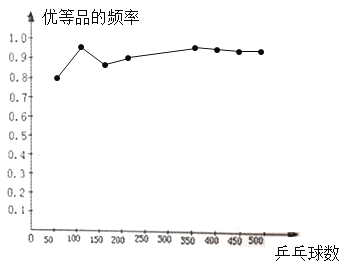
(3)由表中数据可判断优等品频率在0.90左右摆动,于是利于频率估计概率可得这批乒乓球优等品概率的估计值是0.90.

练习册系列答案
相关题目
【题目】简单多面体是各个面都是多边形组成的几何体,十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的关系式,称为欧拉公式.如表是根据左边的多面体模型列出的不完整的表:
多面体 | 顶点数 | 面数 | 棱数 |
四面体 | 4 | 4 | 6 |
长方体 | 8 | 6 | |
正八面体 | 8 | 12 |
现在有一个多面体,它的每一个面都是三角形,它的面数(F)和棱数(E)的和为30,则这个多面体的顶点数V=_____.