题目内容
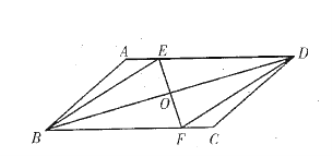
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:连接OA,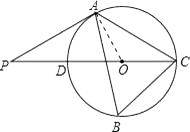
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2 ![]() ,
,
∴BE= ![]() BC=
BC= ![]() ,CE=3,
,CE=3,
∵AB=4+ ![]() ,
,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC= ![]() =5,
=5,
∴AP=AC=5.
∴在Rt△PAO中,OA= ![]() ,
,
∴⊙O的半径为 ![]() .
.
【解析】(1)连接半径,利用圆周角定理和等腰三角形的性质可证出OA⊥PA,进而证出PA是⊙O的切线;(2)通过过C作垂线把∠B放到直角三角形中,利用60度角的三角函数,求出AC,进而求出⊙O的半径.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表![]() 单位:环
单位:环![]() :
:
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
甲 | 10 | 9 | 8 | 8 | 10 | 9 |
乙 | 10 | 10 | 8 | 10 | 7 | 9 |
根据表格中的数据,可计算出甲、乙两人的平均成绩都是9环.
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选______名队员参赛.