��Ŀ����
����Ŀ���ۺ���ʵ��
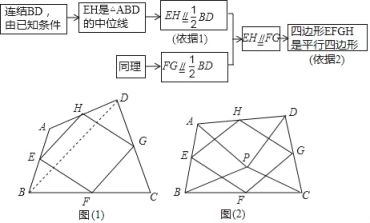
�����龳������ѧ����ϣ����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ���ͼ��1�������ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��˵���е��ı���EFGH��ƽ���ı��Σ�
̽��չʾ���ڷ�С��Ľ���˼·��
��˼������
��1������������˼·�е�������1����������2���ֱ���ʲô��
����1���� ��������2���� ����
������AC����AC��BDʱ�����е��ı���EFGH����״Ϊ�� ����
����С���ܵ��ڷ�С�������������̽����
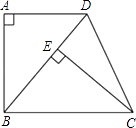
��2����ͼ��2������P���ı���ABCD��һ�㣬������PA��PB��PC��PD����APB����CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����˵�����ɣ�
��3�����ı䣨2���е�������ʹ��APB����CPD��90���������������䣬���е��ı���EFGH����״Ϊ�� ����
���𰸡���1��������1�������ε���λ�߶���������2��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ������Σ����ɼ���������2���ı���EFGH�����Σ����ɼ���������3�������Σ����ɼ�����.
��������
��1��������������λ�߶�����ɣ�
��2������ƽ���ı��ε��ж������ε��ж���ɣ�
��3��������һ������ֱ�ǵ������������μ���֤����
��1��������1�������ε���λ�߶�����
����2��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�
������
���ɣ���ͼ1�У�
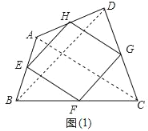
��AE��BE��AH��HD��
��EH��![]() BD��
BD��
��DH��HA��DG��GC��
��HG��![]() AC��
AC��
��HE��HG��
���ı���EFGH��ƽ���ı��Σ�
���ı���EFGH�����Σ�
�ʴ�Ϊ��������λ�߶�����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ����Σ�
��2�����ۣ��ı���EFGH�����Σ�
���ɣ���ͼ2�У�����AC��BD
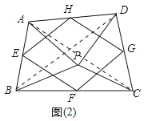
�ߡ�APB����CPD
���APB+��APD����CPD+��APD
������BPD����APC
��PA��PB��PC��PD
���APC�ա�BPD
��AC��BD
��HG��HE
��(1)��֪���ı���EFGH��ƽ���ı���
���ı���EFGH�����Σ�
��3�����ۣ������Σ�
���ɣ���ͼ2��1�У�����AC��BD��BD��AC�ڵ�O����GH�ڵ�K��AC��PD�ڵ�J��
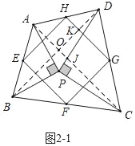
�ߡ�APC�ա�BPD����DPC��90����
���PDB����PCA��
�ߡ�PJC����DJO��
���CPJ����DOJ��90����
��HG��AC��
���BKG����BOC��90����
��EH��BD��
���EHG����BKG��90����
���ı���EFGH�����Σ�
���ı���EFGH�������Σ�

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�