题目内容
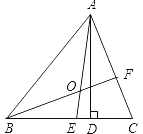
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
【答案】(1) 见解析;(2) AE = ![]() .
.
【解析】分析:(1)在两个三角形中,证明两个三角形全等,找出三角形全等的条件,根据同弧所对的圆周角相等,根据所给的边长相等,由边角边确定两个三角形是全等三角形.
(2)可以证明![]() 得到对应边成比例,设出要求的边长,得到关于边长的方程,解方程即可.
得到对应边成比例,设出要求的边长,得到关于边长的方程,解方程即可.
详解:(1)连接OC,
∵直线MN与⊙O相切于点C,
∴OC ⊥ MN,
∵BD∥ MN,
∴OC ⊥ BD,
∴ ![]() =
=![]() ,
,
∴∠BAE =∠CAD,
在△ABE和△ACD中

∴△ABE ≌ △ACD(ASA).

(2)由(1)知∠BAC = ∠CAD = ∠CBD,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴CE = ![]() ,
,
∴AE = ![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目