题目内容
【题目】如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（ ）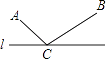
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间，线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
【答案】D
【解析】解：∵点B和点B′关于直线l对称，且点C在l上，
∴CB=CB′，
又∵AB′交l与C，且两条直线相交只有一个交点，
∴CB′+CA最短，
即CA+CB的值最小，
将轴对称最短路径问题利用线段的性质定理两点之间，线段最短，体现了转化思想，验证时利用三角形的两边之和大于第三边．
故选D．
利用两点之间线段最短分析并验证即可即可．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某服装店以每件82元的价格购进了30套保暖内衣，销售时，针对不同的顾客，这30套保暖内衣的售价不完全相同，若以100元为标准，将超过的钱数记为正，不足的钱数记为负，则记录结果如表所示：
售出件数 | 7 | 6 | 7 | 8 | 2 |
售价（元） | +5 | +1 | 0 | ﹣2 | ﹣5 |
请你求出该服装店在售完这30套保暖内衣后，共赚了多少钱？
