��Ŀ����
����Ŀ����ͼ�٣��ھ���ABCD�У�AB��10 cm��BC��8 cm.��P�ӵ�A��������A��B��C��D��·���˶�������Dֹͣ����Q�ӵ�D��������D��C��B��A��·���˶�������Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1 cm����Q���ٶ�Ϊÿ��2 cm��a��ʱ����P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��b cm����Q���ٶȱ�Ϊÿ��d cm.ͼ���ǵ�P����x�����APD�����S1(cm2)��ʱ��x(��)�ĺ�����ϵͼ��ͼ���ǵ�Q����x�����AQD�����S2(cm2)��ʱ��x(��)�ĺ�����ϵͼ����
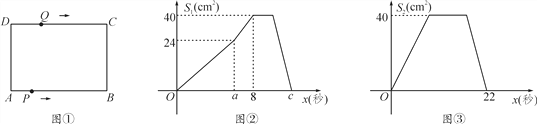
(1)����ͼ�ڣ���a�� b��ͼ����c��ֵ��
(2)��d��ֵ��
(3)���P�뿪��A��·��Ϊy1(cm)����Q����A����Ҫ�ߵ�·��Ϊy2(cm)����ֱ�д���ı��ٶȺ�y1��y2���������˶�ʱ��x(��)�ĺ�����ϵʽ���������P����Q����ʱx��ֵ��
(4)����Q����__ __��ʱ����Q���˶�·��Ϊ25 cm.
���𰸡���1��6��2��17����2��1����3��![]() ����4��1��19.
����4��1��19.
����������������1�����������S��APD���a��b��c��ֵ����2����ͼ����������d�Ĺ�ϵʽ���Ӷ����d����3���������y1��y2����x�ĵ�����ϵ��Ȼ���������ɵ�y1=y2���x��ֵ����4������Q����17��ʱ����P�����Dֹͣ�˶�����Q�����˶�2�룬�����˶�19��ʱ����ʹP��Q���������˶�·��������·��Ϊ25cm��
���������
�⣺(1)�۲�ͼ�ڣ��õ�x��aʱ��S��APD��![]() PA��AD��
PA��AD��![]() a��8��24��
a��8��24��
��a��6��b��![]() ��2��c��8��
��2��c��8��![]() ��17.
��17.
(2)�����⣬��(22��6)d��28��12�����d��1.
(3)y1��2x��6��y2��22��x.����P����Q����ʱ��2x��6��22��x����x��![]() .
.
��4������Q����17��ʱ����P�����Dֹͣ�˶�����Q�����˶�2�룬
�����˶�19��ʱ����ʹP��Q���������˶�·��������·��Ϊ25cm��
��Q����1s�����P��Q���25cm�����Q����x�룬��P����Q���25cm����2x+x=28-25�����x=1��
�൱��Q����1��19��ʱ����P����Q���˶�·��������·��Ϊ25cm��
�ʴ�Ϊ��1��19��

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��