ЬтФПФкШн
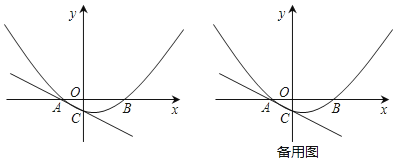
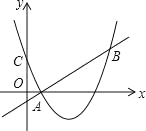
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпC1ЃКy=a(x+2)2-5ЕФЖЅЕуЮЊPЃЌгыxжсЯрНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓБпЃЉЃЌЕуBЕФКсзјБъЪЧ1ЃЎ
(1) ЧѓPЕузјБъМАaЕФжЕЃЛ
(2)ШчЭМЃЈ1ЃЉЃЌ
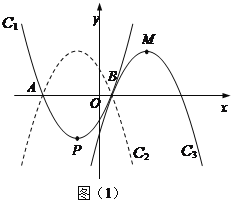
ХзЮяЯпC2гыХзЮяЯпC1ЙигкxжсЖдГЦЃЌНЋХзЮяЯпC2ЯђгвЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпМЧЮЊC3ЃЌC3ЕФЖЅЕуЮЊMЃЌЕБЕуPЁЂMЙигкЕуBГЩжааФЖдГЦЪБЃЌЧѓC3ЕФНтЮіЪНЃЛ
(3) ШчЭМЃЈ2ЃЉЃЌ
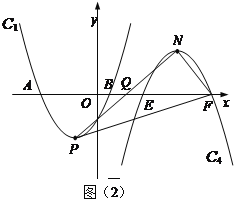
ЕуQЪЧxжсе§АыжсЩЯвЛЕуЃЌНЋХзЮяЯпC1ШЦЕуQа§зЊ180ЁуКѓЕУЕНХзЮяЯпC4ЃЎХзЮяЯпC4ЕФЖЅЕуЮЊNЃЌгыxжсЯрНЛгкEЁЂFСНЕуЃЈЕуEдкЕуFЕФзѓБпЃЉЃЌЕБвдЕуPЁЂNЁЂFЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЕуQЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖЅЕуPЕФЮЊЃЈ-2ЃЌ-5ЃЉЃЌaЃН![]()
ЃЈ2ЃЉХзЮяЯпC3ЕФБэДяЪНЮЊ y=-![]() (x-4)2+5
(x-4)2+5
ЃЈ3ЃЉЕБQЕузјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЪБЃЌвдЕуPЁЂNЁЂFЮЊЖЅЕу
ЃЌ0ЃЉЪБЃЌвдЕуPЁЂNЁЂFЮЊЖЅЕу
ЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЎ
ЁОНтЮіЁП
(1)АбBЃЈ1,0ЃЉДњШыy=a(x+2)2-5ЃЌМДПЩНтЕУaжЕЃЛ
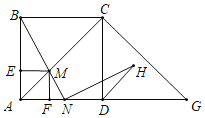
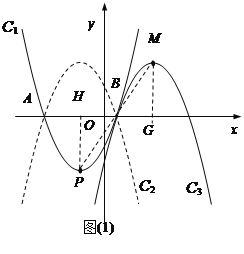
ЃЈ2ЃЉСЌНгPMЃЌзїPHЁЭxжсгкHЃЌзїMGЁЭxжсгкG,ИљОнPЁЂMЙигкЕуBГЩжааФЖдГЦЃЌжЄУїЁїPBHЁеЁїMBGЃЌМДПЩЧѓГіMGЃНPHЃН5ЃЌBGЃНBHЃН3ЃЌЕУЕНЖЅЕуMЕФзјБъЃЌдйИљОнХзЮяЯпC2гЩC1ЙигкxжсЖдГЦЕУЕНЃЌХзЮяЯпC3гЩC2ЦНвЦЕУЕНЃЌМДПЩаДГіХзЮяЯпC3ЕФБэДяЪН
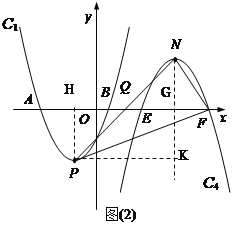
ЃЈ3ЃЉИљОнХзЮяЯпC4гЩC1ШЦЕуxжсЩЯЕФЕуQа§зЊ180ЁуЕУЕНЃЌЕуNЕФзнзјБъЮЊ5ЃЌЩшЕуNЕФзјБъЮЊЃЈm,5ЃЉЃЌзїPHЁЭxжсгкHЃЌзїNGЁЭxжсгкGЃЌзїPKЁЭNGгкKЃЌПЩЧѓГіEFЃНABЃН2BHЃН6ЃЌFGЃН3ЃЌЕуFзјБъЮЊЃЈm+3ЃЌ0ЃЉЃЌHзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌKзјБъЮЊЃЈmЃЌ-5ЃЉЃЌ
ИљОнЙДЙЩЖЈРэЕУPN2ЃНNK2+PK2ЃНm2+4m+104ЃЌPF2ЃНPH2+HF2ЃНm2+10m+50ЃЌNF2ЃН52+32ЃН34ЃЌдйЗжШ§жжЧщПіЬжТлМДПЩ.
(1)гЩХзЮяЯпC1ЃКy=a(x+2)2-5ЃЌЕУ
ЖЅЕуPЕФЮЊЃЈ-2ЃЌ-5ЃЉ
ЁпЕуBЃЈ1ЃЌ0ЃЉдкХзЮяЯпC1ЩЯ
Ёр0= a(1+2)2-5
НтЕУЃЌaЃН![]()
(2)СЌНгPMЃЌзїPHЁЭxжсгкHЃЌзїMGЁЭxжсгкG
ЁпЕуPЁЂMЙигкЕуBГЩжааФЖдГЦ
ЁрPMЙ§ЕуBЃЌЧвPBЃНMB
ЁрЁїPBHЁеЁїMBG
ЁрMGЃНPHЃН5ЃЌBGЃНBHЃН3
ЁрЖЅЕуMЕФзјБъЮЊЃЈ4ЃЌ5ЃЉ
ЁпХзЮяЯпC2гЩC1ЙигкxжсЖдГЦЕУЕНЃЌХзЮяЯпC3гЩC2ЦНвЦЕУЕН
ЁрХзЮяЯпC3ЕФБэДяЪНЮЊ y=-![]() (x-4)2+5
(x-4)2+5
ЃЈ3ЃЉЁпХзЮяЯпC4гЩC1ШЦЕуxжсЩЯЕФЕуQа§зЊ180ЁуЕУЕН
ЁрЖЅЕуNЁЂPЙигкЕуQГЩжааФЖдГЦ
гЩЃЈ2ЃЉЕУЕуNЕФзнзјБъЮЊ5
ЩшЕуNзјБъЮЊЃЈmЃЌ5ЃЉ
зїPHЁЭxжсгкHЃЌзїNGЁЭxжсгкGЃЌзїPKЁЭNGгкK
Ёпа§зЊжааФQдкxжсЩЯ
ЁрEFЃНABЃН2BHЃН6
ЁрFGЃН3ЃЌЕуFзјБъЮЊЃЈm+3ЃЌ0ЃЉЃЌHзјБъЮЊЃЈ2ЃЌ0/span>ЃЉЃЌKзјБъЮЊЃЈmЃЌ-5ЃЉЃЌ
ИљОнЙДЙЩЖЈРэЕУ
PN2ЃНNK2+PK2ЃНm2+4m+104
PF2ЃНPH2+HF2ЃНm2+10m+50
NF2ЃН52+32ЃН34
ЂйЕБЁЯPNFЃН90ЪБЃЌPN2+ NF2ЃНPF2ЃЌНтЕУmЃН![]() ЃЌ
ЃЌ
ЁрQЕузјБъЮЊЃЈ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ЂкЕБЁЯPFNЃН90ЪБЃЌPF2+ NF2ЃНPN2ЃЌНтЕУmЃН![]() ЃЌЁрQЕузјБъЮЊЃЈ
ЃЌЁрQЕузјБъЮЊЃЈ![]() ЃЌ0ЃЉ
ЃЌ0ЃЉ
ЂлЁпPNЃОNKЃН10ЃОNFЃЌЁрЁЯNPFЁй90
злЩЯЫљЕУЃЌЕБQЕузјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЪБЃЌвдЕуPЁЂNЁЂFЮЊЖЅЕу
ЃЌ0ЃЉЪБЃЌвдЕуPЁЂNЁЂFЮЊЖЅЕу
ЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЎ

 ЦкФЉИДЯАМьВтЯЕСаД№АИ
ЦкФЉИДЯАМьВтЯЕСаД№АИ ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ