题目内容
【题目】定义:若存在实数对坐标(x,y)同时满足一次函数y=px+q和反比例函数y=![]() ,则二次函数y=px2+qxk为一次函数和反比例函数的“联姻”函数.
,则二次函数y=px2+qxk为一次函数和反比例函数的“联姻”函数.
(1)试判断(需要写出判断过程):一次函数y=x+3和反比例函数y=![]() 是否存在“联姻”函数,若存在,写出它们的“联姻”函数和实数对坐标.
是否存在“联姻”函数,若存在,写出它们的“联姻”函数和实数对坐标.
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y=![]() 存在“联姻”函数y=(m+t)x2+(10mt)x2015,求m的值.
存在“联姻”函数y=(m+t)x2+(10mt)x2015,求m的值.
(3)若同时存在两组实数对坐标[x1,y1]和[x2,y2]使一次函数y=ax+2b和反比例函数y=![]() 为“联姻”函数,其中,实数a>b>c,a+b+c=0,设
为“联姻”函数,其中,实数a>b>c,a+b+c=0,设![]() ,求L的取值范围.
,求L的取值范围.
【答案】(1)存在,实数对坐标为(1,2),(2,1);(2) m=2;(3) ![]() <L<2
<L<2![]() .
.
【解析】
(1)只需将y=x+3与y=![]() 组成方程组,并求出该方程组的解即可解决问题;
组成方程组,并求出该方程组的解即可解决问题;
(2)根据题意得![]() ,解得
,解得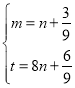 .然后根据t<n<8m求出n的取值范围,进而求出m的取值范围,就可求出整数m的值;
.然后根据t<n<8m求出n的取值范围,进而求出m的取值范围,就可求出整数m的值;
(3)由a>b>c,a+b+c=0可得a>0,c<0,a>ac,ac>c,即可得到(2b)24ac>0,2<![]() <12,由题可得x1+x2=2ba,x1x2=
<12,由题可得x1+x2=2ba,x1x2=![]() ,从而得到
,从而得到
![]() =
=![]() =
=![]() =2
=2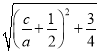 ,利用二次函数的增减性并结合2<
,利用二次函数的增减性并结合2<![]() <
<![]() 即可得到L的取值范围.
即可得到L的取值范围.
(1)联立![]() ,
,
解得![]() 或
或![]() .
.
则一次函数y=x+3和反比例函数y=![]() 存在“联姻”函数,它们的“联姻”函数为y=x2+3x2,实数对坐标为(1,2),(2,1);
存在“联姻”函数,它们的“联姻”函数为y=x2+3x2,实数对坐标为(1,2),(2,1);
(2)根据题意得:![]() ,
,
解得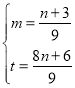 .
.
∵t<n<8m,
∴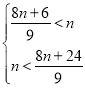
解得6<n<24,
∴9<n+3<27,
∴1< ![]() <3,
<3,
∴1<m<3.
span>∵m是整数,
∴m=2;
(3)∵a>b>c,a+b+c=0,
∴a>0,c<0,a>ac,ac>c,
∴(2b)24ac>0,2<![]() <
<![]()
∴方程ax2+2bx+c=0有两个不相等的实根.
由题可得:x1、x2是方程ax+2b=cx即ax2+2bx+c=0的两个不等实根.
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴L= L=|x1x2|=![]()
=![]()
=![]() =
=![]()
=![]()
=![]() ,
,
∵2<![]() <
<![]() ,
,
∴![]() <L<2
<L<2![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案