题目内容
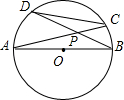 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.(1)设∠BPC=α,如果sinα是方程5x2-13x+6=0的根,求cosα的值;
(2)在(1)的条件下,求弦CD的长.
分析:(1)利用十字相乘法,求得一元二次方程的根,即sinα的值.进而求得cosα的值.
(2)首先连接BC,利用圆周角定理得到∠B=∠C,∠A=∠D,进而证得△APB∽△DPC.再利用相似三角形的性质定理及(1)中的解,求得弦CD的长.
(2)首先连接BC,利用圆周角定理得到∠B=∠C,∠A=∠D,进而证得△APB∽△DPC.再利用相似三角形的性质定理及(1)中的解,求得弦CD的长.
解答:解:(1)∵sinα是方程5x-13x+6=0的根,
解得:sinα=2(舍去),sinα=
,(2分)
∴cosα=
;(1分)
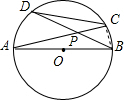
(2)连接BC,
∵∠B=∠C,∠A=∠D,
∴△APB∽△DPC,
∴
=
,(2分)
∵AB为直径,
∴∠BCA为直角,
∵cosα=
,
∴
=
=
,
∴CD=8.(3分)
解得:sinα=2(舍去),sinα=
| 3 |
| 5 |
∴cosα=
| 4 |
| 5 |

(2)连接BC,
∵∠B=∠C,∠A=∠D,
∴△APB∽△DPC,
∴
| CD |
| AB |
| CP |
| PB |
∵AB为直径,
∴∠BCA为直角,
∵cosα=
| 4 |
| 5 |
∴
| CD |
| AB |
| CP |
| PB |
| 4 |
| 5 |
∴CD=8.(3分)
点评:本题考查了解一元一次方程因式分解法、圆周角定理、直角三角形边间的正弦、余弦关系,相似三角形的判定和性质等知识,综合性较强.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 已知:如图,⊙O的直径AB与弦CD相交于E,
已知:如图,⊙O的直径AB与弦CD相交于E,
 如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于
如图,⊙O的直径AB与弦CD(不是直径)相交于E,E是CD的中点,过点B作BF∥CD交AD的延长线于 如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论:
如图,⊙O的直径AB,CD互相垂直,P为 上任意一点,连PC,PA,PD,PB,下列结论: (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC= 如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是
如图,⊙O的直径AB垂直弦CD于P,且P是半径OB的中点,CD=6cm,则直径AB的长是