题目内容
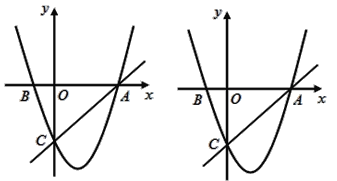
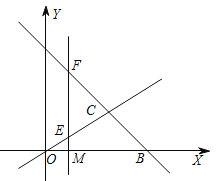
【题目】如图，直线OC，BC的函数关系式分别是y1=
x和y2=-x+6，两直线的交点为C.
（1）求点C的坐标，并直接写出y1＞y2时x的范围；
（2）在直线y1上找点D，使△DCB的面积是△COB的一半，求点D的坐标；
（3）点M（t,0）是
轴上的任意一点，过点M作直线l⊥
轴，分别交直线y1、 y2于点E、F，当E、F两点间的距离不超过4时，求t的取值范围．
【答案】（1）点C的坐标为（4，2），y1＞y2时x的范围x＞4；
（2）点D的坐标为（2，1）或（6，3）；
（3）t的取值范围
【解析】解：（1）解
得： 
，∴ C（4，2）； 由图像可知，当y1＞y2时，x＞4；
（2）显然，当2CD=OC时，△DCB的面积是△COB的一半，∵D在直线y1上，设D（x， 
x），则： 
，解得： 
， 
，∴
， 
，∴D（2，1）或（6，3）；
（3）∵M（t，0），∴E（t， 
t），F（t， - t +6），EF=
，
令
=4， 解得： 
=
， 
=
．由图像可知
练习册系列答案
相关题目
