题目内容
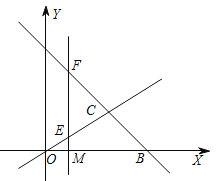
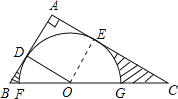
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
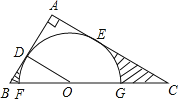
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
【答案】(1)OD=3;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)由AB为圆O的切线,利用切线的性质得到OD垂直于AB,在直角三角形BDO中,利用锐角三角函数定义,根据tan∠BOD及BD的值,求出OD的值即可;
(2)连接OE,由AE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证;
(3)阴影部分的面积由三角形BOD的面积+三角形ECO的面积﹣扇形DOF的面积﹣扇形EOG的面积,求出即可.
解:(1)∵AB与圆O相切,
∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD=![]() =
=![]() ,
,
∴OD=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AE为圆O的切线;
(3)∵OD∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AC=7.5,
∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=![]() ×2×3+
×2×3+![]() ×3×4.5﹣
×3×4.5﹣![]()
=3+![]() ﹣
﹣![]()
=![]() .
.

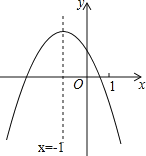
【题目】“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 (辆) | 借车数 (辆) | 存量y (辆) |
6:00﹣7:00 | 1 | 45 | 5 | 100 |
7:00﹣8:00 | 2 | 43 | 11 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:

(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.