题目内容
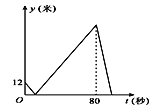
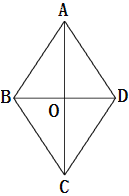
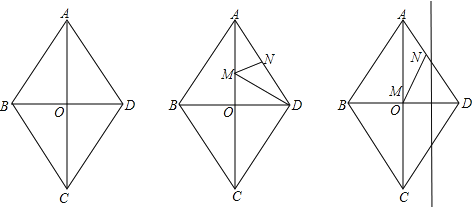
【题目】如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.
【答案】(1)200;(2)480;(3)2,![]() .
.
【解析】
试题分析:本题考查了相似三角形的判定与性质、菱形、等腰三角形、中垂线、勾股定理、解直角三角形、二次函数极值等知识点,涉及考点较多,有一定的难度.第(2)问中,动点M在线段AO和OD上运动时,是两种不同的情形,需要分类讨论;第(3)问中,满足条件的点有2个,注意不要漏解.
(1)根据勾股定理及菱形的性质,求出菱形的周长;
(2)在动点M、N运动过程中:①当0<t≤40时,如答图1所示,②当40<t≤50时,如答图2所示.分别求出S的关系式,然后利用二次函数的性质求出最大值;
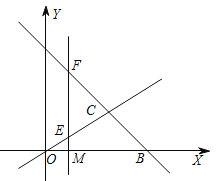
(3)如答图4所示,作ON的垂直平分线,交EF于点I,连接OI,IN.过点N作NG⊥OD,NH⊥EF,垂足分别为G,H.易得△DNG∽△DAO,由EF垂直平分OD,得到OE=ED=15,EG=NH=3,再设OI=R,EI=x,根据勾股定理,在Rt△OEI和Rt△NIH中,得到关于R和x的 方程组,解得R和x的值,把二者相加就是点P到OD的距离,即PE=PI+IE=R+x,又根据对称性可得,在BD下方还存在一个点P′也满足条件,故存在两个点P,到OD的距离也相同,从而问题解决.
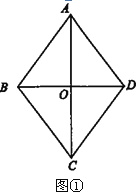
试题解析:(1)如图①)在菱形ABCD中,OA=![]() AC=40, OD=
AC=40, OD=![]() BD=30,
BD=30,
∵AC⊥BD,
∴AD=![]() =50,
=50,
∴菱形ABCD的周长为200;
(2)(如图②)过点M作MH⊥AD于点H.
① (如图②甲)①当0<t≤40时,
∵sin∠OAD=![]() =
=![]() =
=![]() ,
,
∴MH=![]() t,
t,
∴S=![]() DN·MH=
DN·MH=![]() t2.
t2.
②(如图②乙)当40<t≤50时,
∴MD=80-t,
∵sin∠ADO=![]() -
-![]() ,
,
∴MH=![]() (70-t),
(70-t),
∴S=![]() DN·MH,
DN·MH,
=-![]() t2+28t
t2+28t
=-![]() (t-35)2+490.
(t-35)2+490.
∴S=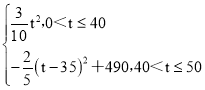 ,
,
当0<t≤40时,S随t的增大而增大,当t=40时,最大值为480.
当40<t≤50时,S随t的增大而增大,当t=40时,最大值为480.
综上所述,S的最大值为480;

(3)存在2个点P,使得∠DPO=∠DON.
(如图④)作ON的垂直平分线,交EF于点I,连接OI,IN.
过点N作NG⊥OD,NH⊥EF,垂足分别为G,H.
当t=30时,DN=OD=30,易知△DNG∽△DAO,
∴NG=24,DG=18.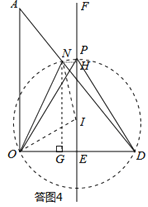
∵EF垂直平分OD,
∴OE=ED=15,EG=NH=3,
设OI=R,EI=x,则
在Rt△OEI中,有R2=152+x2……①,
在Rt△NIH中,有R2=32+(24-x)2……②,
由①,②可得: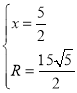 ,
,
∴PE=PI+IE=![]() .
.
根据对称性可得,在BD下方还存在一个点P′也满足条件,
∴存在两个点P,到OD的距离都是![]() .
.