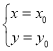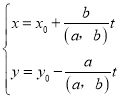题目内容
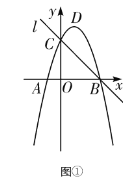
【题目】如图①,已知抛物线y=![]() +bx+c与x轴交于点A、
+bx+c与x轴交于点A、![]() ,与y轴交于点
,与y轴交于点![]() ,直线
,直线![]() 经过B、C两点. 抛物线的顶点为D.
经过B、C两点. 抛物线的顶点为D.
(1)求抛物线和直线![]() 的解析式;
的解析式;
(2)判断△BCD的形状并说明理由.
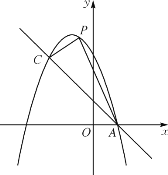
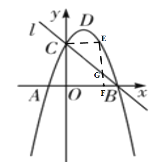
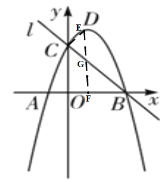
(3)如图②,若点E是线段BC上方的抛物线上的一个动点,过E点作EF⊥x轴于点F,EF交线段BC于点G,当△ECG是直角三角形时,求点E的坐标.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是直角三角形;(3)
是直角三角形;(3)![]() 或
或![]() .
.
【解析】
(1)将点B、点C坐标代入y=![]() +bx+c可得抛物线解析式,设直线BC的解析式为
+bx+c可得抛物线解析式,设直线BC的解析式为![]() ,将点B、点C坐标代入可得直线解析式;
,将点B、点C坐标代入可得直线解析式;
(2)根据抛物线解析式可得点D坐标,由两点间的距离公式求出BC、BD、CD长,可判断出△BCD的形状;
(3)设E点坐标为![]() ,当△ECG是直角三角形时,分①
,当△ECG是直角三角形时,分①![]() ,此时,根据点E和点C纵坐标相同求解即可;②
,此时,根据点E和点C纵坐标相同求解即可;②![]() ,即
,即![]() ,根据直线EC和直线KC的k值乘积为-1,可确定直线EC的解析式,将点E代入求解即可.
,根据直线EC和直线KC的k值乘积为-1,可确定直线EC的解析式,将点E代入求解即可.
解:(1)将点![]() ,点
,点![]() 代入y=
代入y=![]() +bx+c可得
+bx+c可得
![]() ,解得
,解得![]()
![]()
设直线BC的解析式为![]() ,将点B、点C坐标代入得
,将点B、点C坐标代入得
![]() ,解得
,解得![]()
![]()
所以抛物线的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ;
;
(2)![]() 是直角三角形.
是直角三角形.
![]()
![]()
![]()
![]()
![]() 是直角三角形;
是直角三角形;
(3)当△ECG是直角三角形时,设E点坐标为![]() ,
,
①如图,![]() ,此时,点E和点C纵坐标相同,
,此时,点E和点C纵坐标相同,
![]()
解得![]() (舍去)或
(舍去)或![]() ,
,
![]()
②如图,![]() ,即
,即![]() ,
,
设直线EC的解析式为![]()
由点![]() 可知
可知![]() ,
,
![]()
![]()
![]()
![]()
将点E![]() 代入得
代入得![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
![]()
![]() ;
;
综上所述,当△ECG是直角三角形时,点E的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目