题目内容
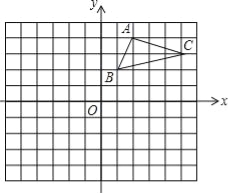
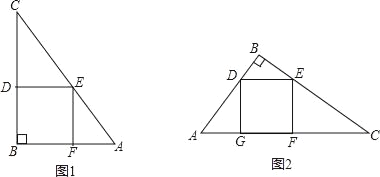
【题目】一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果中可保留分数)
【答案】甲同学设计的方案较好
【解析】试题分析:利用正方形的对边平行.寻找相似三角形,由“相似三角形对应边的比,等于对应边上高的比”的性质,列出等量关系,计算正方形的边长x、y,比较大小,选择合理方案.
试题解析:解:由AB=1.5m,S△ABC=1.5m2,可得BC=2m.
由图1,若设甲设计的正方形桌面边长为xm,由DE∥AB,得Rt△CDE∽Rt△CBA,
∴![]() ,即
,即![]() ,∴3﹣1.5x=2x,x=
,∴3﹣1.5x=2x,x=![]() .
.
由图2,过点B作Rt△ABC斜边AC上的高,BH交DE于P,交AC于H.
由AB=1.5m,BC=2m,得AC=![]() =
=![]() =2.5(m).
=2.5(m).
由ACBH=ABBC可得,BH=![]() =
=![]() =1.2m.
=1.2m.
设乙设计的桌面的边长为ym.
∵DE∥AC,∴Rt△BDE∽Rt△BAC,∴ ![]() ,即
,即![]() ,解得y=
,解得y=![]() .
.
∵![]() =
=![]() >
>![]() ,∴x2>y2,∴甲同学设计的方案较好.
,∴x2>y2,∴甲同学设计的方案较好.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目