题目内容
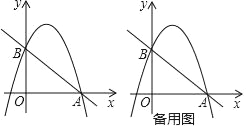
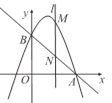
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
【答案】(1) 抛物线的函数表达式是y=﹣x2+2x+3;直线AB的函数表达式是y=﹣x+3;(2) 点M与点N之间的距离有最大值![]() ;点M坐标为(
;点M坐标为(![]() ,
,![]() )点N的坐标为(
)点N的坐标为(![]() ,
,![]() ).
).
【解析】整体分析:
(1)把点B(0,3)和点A(3,0)代入到y=-x2+bx+c和一次函数的一般式中求解;(2)设直线l的横坐标为a,分别用a表示出点M,N的坐标,然后用a表示出MN的长,用配方法即可求出MN的最大值.
解:(1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),
![]() 解得
解得![]()
抛物线的函数表达式是y=-x2+2x+3;
设直线AB:y=kx+m,根据题意得![]() ,解得
,解得![]() ,
,
直线AB的函数表达式是y=-x+3;
(2)如图,设直线l的横坐标为a,
则点M的坐标为(a,-a2+2a+3),点N的坐标是(a,-a+3),
又点M,N在第一象限,
∴|MN|=-a2+2a+3-(-a+3)=-a2+3a,
又|MN|=-a2+3a=-(a2-3a+![]() )+
)+![]() =
=![]() ,
,
当a=![]() 时,|MN|有最大值,最大值为
时,|MN|有最大值,最大值为![]() ,
,
即点M与点N之间的距离有最大值![]() ,
,
此时点M坐标为(![]() ,
,![]() ),点N的坐标为
),点N的坐标为![]() .
.

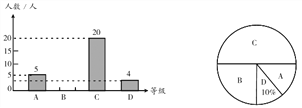
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.