ĢāÄæÄŚČŻ
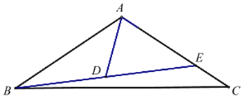
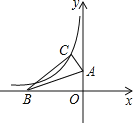
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻߵĽāĪöŹ½ĪŖy£½©![]() x+5£¬Å×ĪļĻßÓėxÖį½»ÓŚA”¢BĮ½µć£ØAµćŌŚBµćµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻ߶Ō³ĘÖįÓėÖ±ĻßBC½»ÓŚµćD£®
x+5£¬Å×ĪļĻßÓėxÖį½»ÓŚA”¢BĮ½µć£ØAµćŌŚBµćµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬Å×ĪļĻ߶Ō³ĘÖįÓėÖ±ĻßBC½»ÓŚµćD£®
£Ø1£©EµćŹĒĻ߶ĪBCÉĻ·½Å×ĪļĻßÉĻŅ»µć£¬¹żµćE×÷Ö±ĻßEFĘ½ŠŠÓŚyÖį£¬½»BCÓŚµćF£¬ČōĻ߶ĪCD³¤¶Č±£³Ö²»±ä£¬ŃŲÖ±ĻßBCŅĘ¶ÆµĆµ½C'D'£¬µ±Ļ߶ĪEF×ī“óŹ±£¬ĒóEC'+C'D'+![]() D'BµÄ×īŠ”Öµ£»
D'BµÄ×īŠ”Öµ£»
£Ø2£©QŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ĒėĪŹÅ×ĪļĻ߶Ō³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćPŹĒ”÷APQĪŖµČ±ßČż½ĒŠĪ£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öČż½ĒŠĪ±ß³¤£¬Čō²»“ęŌŚĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©“ęŌŚ£¬Āś×ćŅŖĒóµÄµČ±ßČż½ĒŠĪµÄ±ß³¤æÉŅŌŹĒ£ŗ6
£»£Ø2£©“ęŌŚ£¬Āś×ćŅŖĒóµÄµČ±ßČż½ĒŠĪµÄ±ß³¤æÉŅŌŹĒ£ŗ6![]() ”¢2
Ӣ2![]() Ӣ2
”¢2![]() £®
£®
”¾½āĪö”æ
£Ø1£©øł¾Ż½āĪöŹ½°Ń±ŲŅŖµÄµćµÄ×ų±ź¼°Ļ߶Ī³¤¶ČĒó³öĄ“±øÓĆ£®½«Eµćŗį×ų±źÉčĪŖĪ“ÖŖŹż£¬ÓĆE”¢FµÄׯ×ų±źÖ®²ī±ķŹ¾EF³¤¶Č£¬ĶعżÅä·½ĒóEFµÄ×īÖµ¼°Č”µĆ×īÖµŹ±Eµć×ų±ź£®ÓÉÓŚC'D'³¤¶Č²»±ä£¬Ņņ“Ė½«EC'Ę½ŅĘÖĮE'D'£¬×¢Ņāµ½”ĻCBOŹĒ30”ć£¬×÷D'G”ĶOBÓŚG£¬E'H”ĶOBÓŚH£¬øł¾Ż“¹Ļ߶Ī×ī¶ĢŌĄķ¼“æÉČ·¶Ø×īÖµ£®
£Ø2£©Ķ¼ŠĪÓŠĖÄÖÖĒéæö£¬·Ö±š½ųŠŠ¹¹Ķ¼Ēó½ā£®µ±QÓėBÖŲŗĻŹ±¶ŌÓ¦Į½ÖÖĶ¼£ØPµ½xÉĻ·½ŗĶĻĀ·½£©£¬ÕāĮ½ÖÖĒéæöµÄµČ±ßČż½ĒŠĪµÄ±ß³¤ŹĒŅ»ŃłµÄ£¬¾ĶŹĒABµÄ³¤£»µŚČżÖÖĒéæö£¬QÓėCÖŲŗĻ£¬“ĖŹ±µÄµČ±ßČż½ĒŠĪ±ß³¤¾ĶŹĒAC³¤¶Č£ØÕāÖÖĒéæöĻĀ£¬PĘ䏵¾ĶŹĒ”÷ABCµÄĶāŠÄ£©£»µŚĖÄÖÖĒéæö£¬QŌŚµŚČżĻóĻŽ£¬ÓÉÓŚPQ£½PA£½PB£¬øł¾ŻŌ²ÖܽĒÓėŌ²ŠÄ½ĒµÄ¹ŲĻµæɵƔĻABQ£½30”ć£¬ÓŚŹĒæÉĒó³öBQ½āĪöŹ½£¬½«BQ½āĪöŹ½ÓėÅ×ĪļĻß½āĪöŹ½ĮŖĮ¢·½³Ģ×éæɽā³öQµć×ų±ź£¬Č»ŗóÓÉĮ½µć¼äµÄ¾ąĄė¹«Ź½Ēó³öAQ³¤¶Č¾ĶŹĒ¶ŌÓ¦µÄµČ±ßČż½ĒŠĪµÄ±ß³¤£®
½ā£ŗ£Ø1£©ŅņĪŖy£½©![]() x2+
x2+![]() x+5£½©
x+5£½©![]() £Øx©5
£Øx©5![]() £©£Øx+
£©£Øx+![]() £©£¬
£©£¬
”ąA£Ø©![]() £¬0£©£¬B£Ø5
£¬0£©£¬B£Ø5![]() £¬0£©£¬C£Ø0£¬5£©£¬Å×ĪļĻ߶Ō³ĘÖįĪŖx£½
£¬0£©£¬C£Ø0£¬5£©£¬Å×ĪļĻ߶Ō³ĘÖįĪŖx£½![]() £½2
£½2![]() £¬
£¬
ÓÉB”¢C×ų±źæÉĒóµĆÖ±ĻßBCµÄ½āĪöŹ½ĪŖy£½©![]() x+5£¬
x+5£¬
Įīx£½2![]() £¬Ōņy£½©
£¬Ōņy£½©![]() ”Į2
”Į2![]() +5£½3£¬
+5£½3£¬
”ąD£Ø2![]() £¬3£©£¬
£¬3£©£¬
”ąCD£½C'D'£½4£®
ÉčE£Øm£¬©![]() m2+
m2+![]() m+5£©£¬ŌņF£Øm£¬©
m+5£©£¬ŌņF£Øm£¬©![]() m+5£©£¬
m+5£©£¬
”ąEF£½yE©yF£½©![]() m2+
m2+![]() m+5+
m+5+![]() m©5£½©
m©5£½©![]() m2+
m2+![]() m£½©
m£½©![]() £Øm©
£Øm©![]() £©2+
£©2+![]() £¬
£¬
”ąµ±m£½![]() Ź±£¬EFČ”µĆ×ī“óÖµ
Ź±£¬EFČ”µĆ×ī“óÖµ![]() £¬“ĖŹ±E£Ø
£¬“ĖŹ±E£Ø![]() £¬
£¬![]() £©£®
£©£®
ČēĶ¼1£¬×÷Ę½ŠŠĖıߊĪEC'D'E'£¬ŌņEC'£½E'D'£¬E'£Ø![]() £¬
£¬![]() £©£®
£©£®
×÷D'G”ĶOBÓŚG£¬E'H”ĶOBÓŚH£®
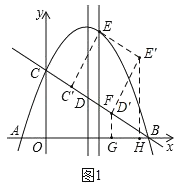
”ßtan”ĻCBO£½![]() £½
£½![]() £½
£½![]() £¬ĖłŅŌ”ĻCBO£½30”ć£¬
£¬ĖłŅŌ”ĻCBO£½30”ć£¬
”ąD'G£½![]() D'B£¬
D'B£¬
”ąEC'+C'D'+D'B£½C'D'+E'D'+D'G”ŻC'D'+E'H£¬
µ±ĒŅ½öµ±E'”¢D'”¢GČżµć¹²Ļߏ±£¬
EC'+C'D'+![]() D'BČ”µĆ×īŠ”ÖµC'D'+E'H£½4+
D'BČ”µĆ×īŠ”ÖµC'D'+E'H£½4+![]() £½
£½![]() £®
£®
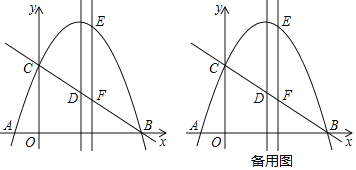
£Ø2£©¢ŁČēĶ¼2£¬”÷APQŹĒµČ±ßČż½ĒŠĪ£¬“ĖŹ±QÓėBÖŲŗĻ£¬
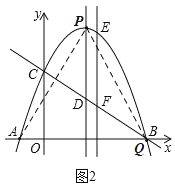
”ąµČ±ßČż½ĒŠĪµÄ±ß³¤ĪŖAQ£½AB£½6![]() £®
£®
¢ŚČēĶ¼3£¬”÷APQŹĒµČ±ßČż½ĒŠĪ£¬“ĖŹ±QÓėBÖŲŗĻ£¬PŌŚxÖįĻĀ·½£®

”ąµČ±ßČż½ĒŠĪµÄ±ß³¤ĪŖAQ£½AB£½6![]() £®
£®
¢ŪČēĶ¼4£¬”÷APQŹĒµČ±ßČż½ĒŠĪ£¬“ĖŹ±QÓėCÖŲŗĻ£¬PŌŚxÖįÉĻ·½£®
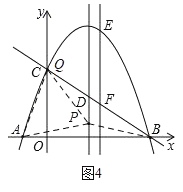
”ąµČ±ßČż½ĒŠĪµÄ±ß³¤ĪŖAQ£½AC£½2![]() £®
£®
¢ÜČēĶ¼5£¬”÷APQŹĒµČ±ßČż½ĒŠĪ£¬“ĖŹ±QŌŚµŚČżĻóĻŽ£¬PŌŚxÖįĻĀ·½£®
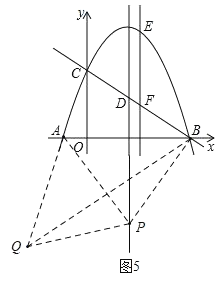
”ßPA£½PB£½PQ£¬ĖłŅŌA”¢Q”¢BČżµćŌŚŅŌPĪŖŌ²ŠÄPAĪŖ°ė¾¶ĪŖŌ²ÖÜÉĻ£¬
”ą”ĻABQ£½![]() ”ĻAPQ£½30”ć£¬
”ĻAPQ£½30”ć£¬
”ąÖ±ĻßBQµÄ½āĪöŹ½ĪŖy£½![]() x©5£¬
x©5£¬
ĮŖĮ¢·½³Ģ×é £¬
£¬
½āµĆ »ņ
»ņ £ØÉį£©£¬
£ØÉį£©£¬
”ąQ£½£Ø©2![]() £¬©7£©£¬
£¬©7£©£¬
”ąAQ£½2![]() £¬¼“µČ±ß”÷APQµÄ±ß³¤ĪŖ2
£¬¼“µČ±ß”÷APQµÄ±ß³¤ĪŖ2![]() £®
£®
×ŪÉĻĖłŹö£¬Āś×ćŅŖĒóµÄµČ±ßČż½ĒŠĪµÄ±ß³¤æÉŅŌŹĒ£ŗ6![]() ”¢2
Ӣ2![]() Ӣ2
”¢2![]() £®
£®

 æŚĖćĢāĢģĢģĮ·ĻµĮŠ“š°ø
æŚĖćĢāĢģĢģĮ·ĻµĮŠ“š°ø”¾ĢāÄæ”抔Ķõµē×Ó²śĘ·×عńŅŌ20ŌŖ/ø±µÄ¼ŪøńÅś·¢ĮĖijŠĀæī¶ś»ś£¬ŌŚŹŌĻśµÄ60ĢģÄŚÕūĄķ³öĮĖĻśŹŪŹż¾ŻČēĻĀ
ĻśŹŪŹż¾Ż(µŚxĢģ) | ŹŪ¼Ū(ŌŖ) | ČÕĻśŹŪĮæ(ø±) |
1”Üx£¼35 | x+30 | 100©2x |
35”Üx”Ü60 | 70 | 100©2x |
(1)ČōŹŌĻś½×¶ĪĆæĢģµÄĄūČóĪŖWŌŖ£¬Ēó³öWÓėxµÄŗÆŹż¹ŲĻµŹ½£»
(2)ĒėĪŹŌŚŹŌĻś½×¶ĪµÄÄÄŅ»ĢģĻśŹŪĄūČóWæÉŅŌ“ļµ½×ī“óÖµ£æ×ī“óÖµĪŖ¶ąÉŁ£æ
”¾ĢāÄæ”æ2019Äź10ŌĀ10ČÕ°ųĶķ18£ŗ10×óÓŅ£¬½ĖÕŹ”ĪŽĪżŹŠÉ½Ēų312¹śµĄÉĻŗ£·½ĻņK135“¦£¬ĪżøŪĀ·ÉĻæēĒųöĻÖĒÅĆę²ą·£¬Ōģ³É3ČĖĖĄĶö£¬2ČĖŹÜÉĖ£¬¾”¹ÜøĆŹĀ¹ŹŌŅņ³õ²½·ÖĪöĪŖ°ė¹ŅĒ£Ņż³µŃĻÖŲ³¬ŌŲµ¼ÖĀĒÅĮŗ·¢Éś²ą·£¬µ«ŹĒŅ²ŅżĘšĮĖÉē»įø÷½ē¶ŌĒÅĮŗÉč¼Ę°²Č«ŠŌµÄµ£ÓĒ£¬ĪŅŹŠ»ż¼«æŖÕ¹¶ŌĒÅĮŗ½į¹¹Éč¼ĘµÄ°²Č«ŠŌ½ųŠŠĘĄ¹Ą£ØŅŃÖŖ£ŗæ¹Ēćø²ĻµŹżŌ½øߣ¬°²Č«ŠŌŌ½Ē棻µ±æ¹Ēćø²ĻµŹż”Ż2£®5Ź±£¬ČĻĪŖøĆ½į¹¹°²Č«£©£¬ĻÖŌŚÖŲĒģŹŠĖ껜³éČ”ĮĖ¼×”¢ŅŅĮ½øöÉč¼ĘŌŗ£¬¶ŌĘäø÷×ŌŌŚ½ØµÄ»ņŅŃ½ØµÄ20׳ĒÅĮŗĻīÄæ½ųŠŠÅŲ飬½«µĆµ½µÄæ¹Ēćø²Źż¾Ż½ųŠŠÕūĄķ”¢ĆčŹöŗĶ·ÖĪö£Øæ¹Ēćø²Źż¾ŻÓĆx±ķŹ¾£¬¹²·Ö³É6×é£ŗA£®0”Üx£¼2£®5£¬B£®2£®5”Üx£¼5£®0£¬C£®5£®0”Üx£¼7£®5£¬D£®7£®5”Üx£¼10£®0£¬E£®10£®0”Üx£¼12£®5£¬F£®12£®5”Üx£¼15£©£¬ĻĀĆęøų³öĮĖ²æ·ÖŠÅĻ¢£»
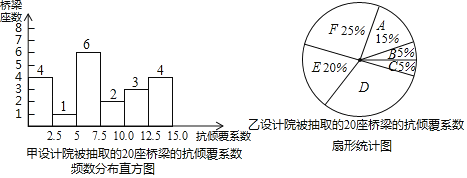
ĘäÖŠ£¬¼×Éč¼ĘŌŗC×éµÄæ¹Ēćø²ĻµŹżŹĒ£ŗ7£¬7£¬7£¬6£¬7£¬7£»
ŅŅÉč¼ĘŌŗD×éµÄæ¹Ēćø²ĻµŹżŹĒ£ŗ8£¬8£¬9£¬8£¬8£¬8£»
¼×”¢ŅŅÉč¼ĘŌŗ·Ö±š±»³éČ”µÄ20׳ĒÅĮŗµÄæ¹Ēćø²ĻµŹżĶ³¼Ę±ķ
Éč¼ĘŌŗ | ¼× | ŅŅ |
Ę½¾łŹż | 7.7 | 8.9 |
ÖŚŹż | a | 8 |
ÖŠĪ»Źż | 7 | b |
·½²ī | 19.7 | 18.3 |
øł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ÉČŠĪĶ³¼ĘĶ¼ÖŠD×鏿¾ŻĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒŹĒ”” ””¶Č£¬a£½”” ””£¬b£½”” ””£»
£Ø2£©øł¾ŻŅŌÉĻŹż¾Ż£¬¼×”¢ŅŅĮ½øöÉč¼ĘŌŗÖŠÄÄøöÉč¼ĘŌŗµÄĒÅĮŗ°²Č«ŠŌøüøߣ¬ĖµĆ÷ĄķÓÉ£ØŅ»Ģõ¼“æÉ£©£ŗ”” ””£»
£Ø3£©¾ŻĶ³¼Ę£¬2018ÄźÖĮ2019Äź£¬¼×Éč¼ĘŌŗĶź³ÉÉč¼Ę80׳ĒÅĮŗ£¬ŅŅÉč¼ĘŌŗĶź³ÉÉč¼Ę120׳ĒÅĮŗ£¬Ēė¹ĄĖć2018ÄźÖĮ2019ÄźĮ½Éč¼ĘŌŗµÄ²»°²Č«ĒÅĮŗµÄ×ÜŹż£®