��Ŀ����
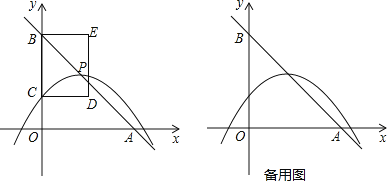
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B��������
��x�ᡢy��ֱ��ڵ�A��B��������![]() �Ķ���P��ֱ��
�Ķ���P��ֱ��![]() ��
��![]() ��P�����B�غ�
��P�����B�غ�![]() ����y�ύ�ڵ�C����BCΪ��������BCDE����
����y�ύ�ڵ�C����BCΪ��������BCDE����![]() ����P��D��y���ͬ�࣮
����P��D��y���ͬ�࣮
![]() ��գ���B������Ϊ______����P������Ϊ______��
��գ���B������Ϊ______����P������Ϊ______��![]() ______
______![]() �ú�m�Ĵ���ʽ��ʾ
�ú�m�Ĵ���ʽ��ʾ![]() ��
��
![]() ����P�ڵ�һ����ʱ�������BCDE�����S��m�ĺ�������ʽ��
����P�ڵ�һ����ʱ�������BCDE�����S��m�ĺ�������ʽ��
![]() ����P��ֱ��
����P��ֱ��![]() �������ƶ�ʱ��������BCDE���������������������ϣ���ֱ��д������������m��ֵ��
�������ƶ�ʱ��������BCDE���������������������ϣ���ֱ��д������������m��ֵ��
���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
![]() ��B����������y��Ľ��㣬��
��B����������y��Ľ��㣬��![]() ����ã�P�������ߵĶ��㣬����ֱ���ϣ����Ը������ʽ��д��
����ã�P�������ߵĶ��㣬����ֱ���ϣ����Ը������ʽ��д��![]() ������ֱ��
������ֱ��![]() ����
����![]() ��
��
![]() ���������ߵĽ���ʽ��ʾBC�ij������þ�������ɵ�S��m�ĺ�������ʽ��
���������ߵĽ���ʽ��ʾBC�ij������þ�������ɵ�S��m�ĺ�������ʽ��
![]() ��C��D����������ʱ����
��C��D����������ʱ����![]() ��֪�Գ���Ϊ
��֪�Գ���Ϊ![]() ����
����![]() ��
��![]() ��C��E����������ʱ����
��C��E����������ʱ����![]() ��
��![]() ��
��![]() �����������߽���ʽ����֮�ɵô𰸣�
�����������߽���ʽ����֮�ɵô𰸣�
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��
![]() ��������
��������![]() �Ķ���P��
�Ķ���P��
![]() ��
��
![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��
![]() ��
��
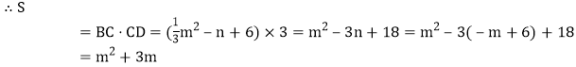 ��
��
![]() ��ͼ
��ͼ![]() ����C��D����������ʱ����
����C��D����������ʱ����![]() ��֪�Գ���Ϊ
��֪�Գ���Ϊ![]() ����
����![]() ��
��
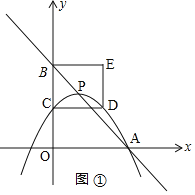
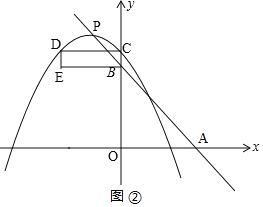
��ͼ![]() ����C��E����������ʱ��
����C��E����������ʱ��
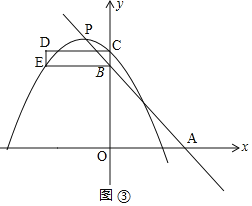
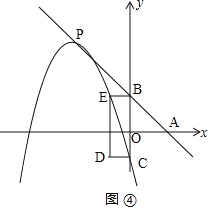
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
![]() ��
��
��ã�![]() ��
��
����������![]() ��
��![]() ��
��![]() ��
��![]() ��
��

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�����Ŀ��С����Ͷ�����ӣ��ʵؾ��ȵ������壩ʵ�飬������50�����飬����¼�����ݽ������������������µ�ͳ�Ʊ���
���ϵĵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
���ֵĴ��� | 7 | 8 |
| 9 | 9 | 7 |
Ƶ�� | 0.14 |
| 0.20 | 0.18 | 0.18 | 0.14 |
(1)�ϱ��У�![]() =______,
=______,![]() =_______��
=_______��
(2)������������ʵ���Сӱ��С������һ����Ϸ�����˷ֱ���һ�����ӣ�˭���������ӳ��ϵĵ������˭�ͻ�ʤ����С�������������ĵ���Ϊ4����ֱ����С����Сӱ��ʤ�ĸ��ʣ�