题目内容
【题目】用一条直线分割一个三角形，如果能分割出等腰三角形，那么就称这条直线为该三角形的一条等腰分割线．在直角三角形ABC中，∠C＝90°，AC＝8，BC＝6．
（1）如图（1），若 O 为 AB 的中点，则直线 OC_____△ABC 的等腰分割线（填“是”或“不是”）
（2）如图（2）已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P，且 PB＝PA，请求出 CP 的长度．
（3）如图（3），在△ABC 中，点 Q 是边 AB 上的一点，如果直线 CQ 是△ABC 的等腰分割线，求线段BQ 的长度等于 ______．（直接写出答案）．
【答案】（1）是；（2）
；（3）5 或 2 或 6 或
【解析】
（1）根据直角三角形斜边上的中线等于斜边的一半可得结论；
（2）设 CP＝x，则 PA＝PB＝8﹣x，根据勾股定理列方程得：62+x2＝(8﹣x)2，求解即可；
（3）分情况进行讨论：
①当△ACQ 是等腰三角形时，分三种情况讨论；
②当△BCQ 是等腰三角形时，同理分三种情况讨论．
解：（1）是，如图（1），
∵∠ACB＝90°，O 为 AB 中点，
∴在Rt△ACB中，OC＝
AB＝AO＝BO，
∴可得到等腰△AOC和等腰△BOC，
∴直线OC是△ABC的等腰分割线，
故答案为：是；
（2）由题可知PA＝PB，BC＝6，
设CP＝x，则PA＝PB＝8﹣x，
在Rt△BPC 中，BC2+PC2＝PB2，
∴62+x2＝（8﹣x）2，
解得：x＝，即：CP＝；
（3）BQ＝2或5或或6，
①若△ACQ 为等腰三角形，
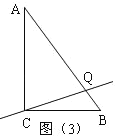
如图（3），当 AC＝AQ 时，AQ＝8，BQ＝AB﹣AQ＝2，
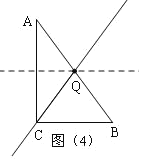
如图（4），当QC＝QA 时，Q为AB中点，BQ＝AB＝5，
当CA＝CQ 时，Q不在线段AB上，舍去；
②若△BCQ 为等腰三角形．
如图（5），当CQ＝CB时，过C作CM⊥AB于M，此时M为BQ的中点，
∵S△ABC＝BCAC＝ABCM，
∴×6×8＝×10CM
解得：CM＝
．
在Rt△CMB中，BM＝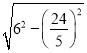
＝
，
∴BQ＝2QM＝，
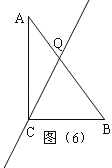
如图（6），当BC＝BQ时，BQ＝BC＝6．
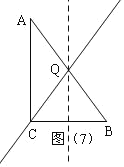
如图（7），当QC＝QB时，Q为AB中点，BQ＝AB＝5．
综上，BQ＝2或5或或6．
