��Ŀ����
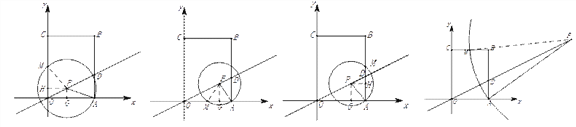
����Ŀ����ͼ1��ֱ������ϵ����һ����OABC������O������ԭ�㣬��A��C�ֱ���x���y���ϣ���B������Ϊ��3��4����ֱ��![]() ��AB�ڵ�D����P��ֱ��
��AB�ڵ�D����P��ֱ��![]() λ�ڵ�һ�����ϵ�һ�㣬����PA����PAΪ�뾶����P��
λ�ڵ�һ�����ϵ�һ�㣬����PA����PAΪ�뾶����P��
��1������AC������P����AC��ʱ�� ��PA�ij���
��2������P������Oʱ����֤����PAD�ǵ��������Σ�
��3�����P�ĺ�����Ϊm��
���ڵ�P�ƶ��Ĺ����У�����P�����OABCijһ�ߵĽ���ǡΪ�ñߵ��е�ʱ������������Ҫ���mֵ��
����ͼ2���ǡ�P��ֱ��![]() ����������ֱ�ΪE��F����E�ڵ�P���·�������DE��DF����
����������ֱ�ΪE��F����E�ڵ�P���·�������DE��DF����![]() ʱ����m��ȡֵ��Χ.����ֱ��д���𰸣�
ʱ����m��ȡֵ��Χ.����ֱ��д���𰸣�

���𰸡���1��![]() ����2����PAD�ǵ��������Σ�֤������������3����
����2����PAD�ǵ��������Σ�֤������������3����![]() ��
�� ![]() ��2��
��2��![]() ����
����![]()
�������������������1��ͨ��֤����OPC�ס�ADP������⣻
��2����OP=AP�á�POA=��PAO����֤��PDA=��DAP���ʿɵ���PAD�ǵ��������� ��
��3����4������������ۼ������.
�����������1����B��3��4��
��BC=3��AB=4
�ߡ�B=90��
��AC=5 ��
��OC��AB��
���OPC�ס�ADP
��![]() ����
����![]()
��![]()
��2���ߡ�P������O
��OP=AP
���POA=��PAO��
�ߡ�PDA+��POA=��DAP+��PAO��
���PDA=��DAP
���PAD�ǵ���������
��3���ٷ�4����������
��������M��OC�е㣬PM=PA
��![]() ��
�� ![]()
��������M��OA�е㣬PM=PA
��MG=GA=![]()
��![]()
��������M��AB�е㣬PM=PA
��PG=![]() AM=1
AM=1
��PH=2DH=2��![]() =1
=1
��![]()
��������M��BC�е㣬PM=PA
��![]() ��
�� ![]()
��![]()

 ��У����ϵ�д�
��У����ϵ�д�
