题目内容
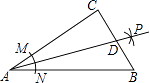
【题目】小敏尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②); 再沿过D点的直线折叠, 使得 C点落在DA边上的点N处, E点落在AE边上的点M处,折痕为 DG(如图).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长与宽的比值为( )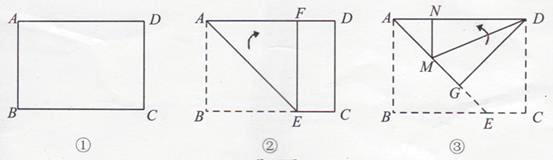
A.2
B.3
C.![]()
D.![]()
【答案】C
【解析】解:连接DE,如图,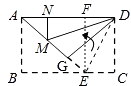
∵沿过A点的直线折叠,使得B点落在AD边上的点F处,
∴四边形ABEF为正方形,
∴∠EAD=45°,
由第二次折叠知,M点正好在∠NDG的平分线上,
∴DE平分∠GDC,
∴Rt△DGE≌Rt△DCE,
∴DC=DG,
又∵△AGD为等腰直角三角形,
∴AD= ![]() DG=
DG= ![]() CD,
CD,
∴矩形ABCD长与宽的比值= ![]() .
.
故选C.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目
【题目】甲,乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)将下表填完整:
身高 | 176 | 177 | 178 | 179 | 180 |
甲队(人数) | 3 | 4 | |||
乙队(人数) | 2 | 1 | 1 |
(2)甲队队员身高的平均数为cm,乙队队员身高的平均数为cm;
(3)你认为哪支仪仗队更为整齐?简要说明理由.