题目内容
【题目】如图,已知在△ABC中,AB=AC=10cm,BC=8cm,D为AB中点,设点P在线段BC上以3cm/秒的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.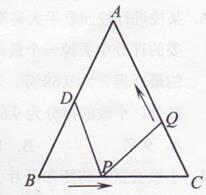
(1)若Q点运动的速度与P点相同,且点P,Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P,Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
(3)若点Q以(2)中的速度从点C出发,点P以原来的速度从点B同时出发,都是逆时针沿△ABC的三边上运动,经过多少时间点P与点Q第一次在△ABC的哪条边上相遇?
【答案】
(1)
解:∵t=1秒,
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中, 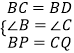
∴△BPD≌△CQP(SAS).
(2)
解:∵vP≠vQ,∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间 ![]() 秒,
秒,
∴vQ= ![]() cm/秒;
cm/秒;
(3)
设经过x秒后点P与点Q第一次相遇,
由题意,得 ![]() x=3x+2×10,
x=3x+2×10,
解得x= ![]() .
.
∴点P共运动了 ![]() ×3=80cm.
×3=80cm.
∴80=56+24=2×28+24,
∴点P、点Q在AB边上相遇,
∴经过 ![]() 秒点P与点Q第一次在边AB上相遇.
秒点P与点Q第一次在边AB上相遇.
【解析】(1)由P,Q的速度相等,t=1秒时,CQ=BP=3cm,易得BD=CP=5,由AB=AC,则∠B=∠C,可证得△BPD≌△CQP;(2)△BPD与△CQP全等时,B与C对应,而vP≠vQ , 则BP≠CQ,则P不与Q对应,则P与P对应,即△BPD≌△CPQ,则BP=PC=4cm,CQ=BD=5cm,所以求出时间,再求Q的速度即可;(3)可设经过x秒后点P与点Q第一次相遇,点Q的速度大于点P,则是Q追P的问题,点Q与点P相距AC+AB=20cm,数量关系:点Q的路程=点P的路程+20,解出时间,则求出P点的路程,算出P绕△ABC运动几周余多少米,可算出点P在哪个位置.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).