题目内容
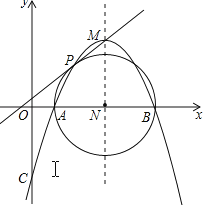
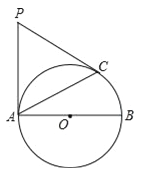
【题目】已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=6,求PA的长.
【答案】(1)∠P=60°;(2)![]() .
.
【解析】
试题分析:(1)由圆的切线的性质,得∠PAB=90°,结合∠BAC=30°得∠PAC=90°﹣30°=60°.由切线长定理得到PA=PC,得△PAC是等边三角形,从而可得∠P=60°.
(2)连接BC,根据直径所对的圆周角为直角,得到∠ACB=90°,结合Rt△ACB中AB=6且∠BAC=30°,得到AC=ABcos∠BAC=![]() .最后在等边△PAC中,可得PA=AC=
.最后在等边△PAC中,可得PA=AC=![]() .
.
试题解析:(1)∵PA是⊙O的切线,AB为⊙O的直径,∴PA⊥AB,即∠PAB=90°.
∵∠BAC=30°,∴∠PAC=90°﹣30°=60°.
又∵PA、PC切⊙O于点A、C,∴PA=PC,∴△PAC是等边三角形,∴∠P=60°;
(2)如图,连接BC.
∵AB是直径,∠ACB=90°,∴在Rt△ACB中,AB=6,∠BAC=30°,可得AC=ABcos∠BAC=6×cos30°=![]() .
.
又∵△PAC是等边三角形,∴PA=AC=![]() .
.


练习册系列答案
相关题目