Question

【题目】已知∠AOB=120°，OC、OD过点O的射线，射线OM、ON分别平分∠AOC和∠DOB．

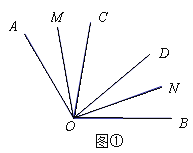
（1）如图①，若OC、OD是∠AOB 的三等分线，求∠MON的度数；

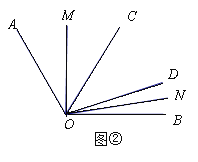
（2）如图②，若∠COD=50°，∠AOC≠∠DOB，则∠MON= °；

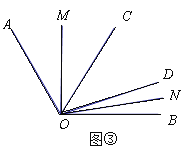
（3）如图③，在∠AOB内，若∠COD=α（0°<α<60°），则∠MON= °.

Answer 1

【答案】（1）∠MON =80°；（2）85°；（3）

【解析】试题分析：（1）根据角平分线的定义得到∠AOC=∠COD=∠DOB=×120°=40°，∠MOC=∠AOC=20°，∠DON=∠DOB=20°，则∠MON=20°+40°+20°=80°；

（2）根据角平分线的定义得到∠MOC=∠AOC，∠DON=∠DOB，而∠AOC+∠DOB=120°-50°=70°，则∠MOC+∠DON=35°，所以∠MON=50°+35°=85°；

（3）与（2）一样得到∠AOC+∠DOB=120°-α，∠MOC+∠DON=60°-α，则∠MON=60°- α+α=60°+α.

试题解析：(1)∵OC，OD是∠AOB的三等分线，

∴∠AOC=∠COD=∠DOB=∠AOB=×120°=40°，

∵OM平分∠AOC，ON平分∠DOB，

∴∠MOC=∠AOC=20°， ∠DON=∠DOB=20° ，

∴∠MON=∠MOC+∠COD+∠DON=80°；

（2）∵射线OM、ON分别平分∠ACO和∠DOB，

∴∠MOC=∠AOC，∠DON=∠DOB，

∴∠MOC+∠DON=（∠AOC+∠DOB），

∵∠AOB=120°，∠COD=50°，

∴∠AOC+∠DOB=120°-50°=70°，

∴∠MOC+∠DON=35°，

∴∠MON=50°+35°=85°，

故答案为：85；

（3）∵射线OM、ON分别平分∠AOC和∠DOB，

∴∠MOC=∠AOC，∠DON=∠DOB，

∴∠MOC+∠DON=（∠AOC+∠DOB），

∵∠AOB=120°，∠COD=α，

∴∠AOC+∠DOB=120°-α，

∴∠MOC+∠DON=60°-α，

∴∠MON=60°-α+α=60°+α= ，

故答案为： .