题目内容
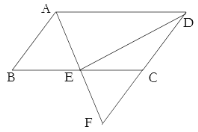
【题目】如图，平行四边形ABCD中，AD=2AB，E是BC的中点，连结AE并延长交DC的延长线于点F．
（1）求证：DE⊥AF；
（2）若∠B=60°，DE=4，求AB的长，
【答案】（1）见解析；（2）
【解析】
（1）先证
ABE≌FCE，得出FC=AB，点E是AF的中点，并推导出FD=AD，得出ADF是等腰三角形，从而证明结论；
（2）∠B=60°，则∠ADE=30°，在RtAED中，可求得AE的长，从而得出AD的长，最后得出AB的长．
（1）∵点E是BC的中点
∴BE=EC
∵四边形ABCD是平行四边形
∴AB∥CD，AB=CD，
∴∠B=∠ECF
在ABE与FCE中
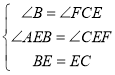
∴ABE≌FCE
∴AB=FC，AE=EF
∵AD=2AB
∴AD=DF，
∴ADF是等腰三角形
∴DE⊥AF
（2）∵∠B=60°
∴∠ADC=60°，
∴∠ADE=30°
∵DE=4，
∴AD=
∴AB=
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
