题目内容
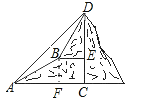
【题目】如图，甲、乙两数学兴趣小组测量山CD 的高度. 甲小组在地面A处测量，乙小组在上坡B处测量，AB=200 m. 甲小组测得山顶D的仰角为45°，山坡B处的仰角为30°；乙小组测得山顶D 的仰角为58°. 求山CD的高度（结果保留一位小数）．参考数据：
，
，供选用.
【答案】山高约为295.2 m.
【解析】
在Rt△AFB中，根据AB=200米，∠BAF=30°，求出BF、AF的长度，然后证明四边形BFCE是矩形，设BE=x米，在Rt△BDE中，用x表示出DE的长度，然后根据AC=DC，代入求出x的值，继而可求得山高．
过B作BF⊥AC于F，
在Rt△AFB中，
∵AB=200米，∠BAF=30°，
∴BF=
AB=×200=100（米），
AF=ABcos30°=100
（米），
∵BF⊥AC，BE⊥DC，
∴四边形BFCE是矩形，
∴EC=BF=100米，
设BE=x米，则FC=x米，
在Rt△DBE中，
∵∠DBE=58°，
∴DE=tan58°BE=1.6x（米），
∵∠DAC=45°，∠C=90°，
∴∠ADC=45°，
∴AC=DC，
∵AC=AF+FC=（100+x）米，
DC=DE+EC=（1.6x+100）米，
解得：x=122，
∴DC=DE+EC=1.6×122+100=295.2（米）；
答：山的高度BC约为295.2米．
练习册系列答案
相关题目
