题目内容
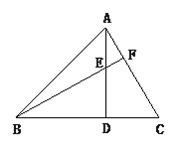
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于E,BD交CE于F.
的中点,CE⊥AB于E,BD交CE于F.
(1)求证:CF=BF
(2)若CD=6,AC=8,求BE、CF的长.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由AB是⊙O的直径得到∠ACB﹦90°,再由CE⊥AB得出∠CEB﹦90° ,即可得出∠BCE﹦∠A ,又由C是弧BD的中点得出∠CBD﹦∠A,根据等量代换得出∠BCF﹦∠CBF,再根据等角对等边得出 CF﹦BF.
(2)根据∠ACB﹦90°、BC=CD=6、AC=8可得出AB= 10,再根据△ABC的面积![]() 可得CE=4.8,在Rt△BEC中CE=4.8,BC=6可得出BE=3.6,设设CF=x,则FE=4.8-x, BF=x,在Rt△BEF中,BE2+EF2=BF2=CF2,即(4.8-x)2+3.62=x2,解方程即可.
可得CE=4.8,在Rt△BEC中CE=4.8,BC=6可得出BE=3.6,设设CF=x,则FE=4.8-x, BF=x,在Rt△BEF中,BE2+EF2=BF2=CF2,即(4.8-x)2+3.62=x2,解方程即可.
试题解析:
(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠BCE﹦∠A
又∵C是弧BD的中点,
∴∠CBD﹦∠A
∴∠BCF﹦∠CBF
∴ CF﹦BF.
(2)∵CD=6,AC=8 ,
∴AB= 10,
∴CE=4.8,
在Rt△BEC中CE=4.8,BC=6
∴BE=3.6,
设CF=x,则FE=4.8-x, BF=x,
∴(4.8-x)2+3.62=x2
∴x=![]()

练习册系列答案
相关题目