��Ŀ����
����Ŀ����ij���⽼һ�����ٹ�·BC�ϣ���·��Ϊֱ�ߣ�����ͨ�������Ź涨�����������ʻ�ٶȲ��ܳ���60ǧ��/ʱ��������ù�·100�״�������һ������A������ͼ��ʾ��ƽ��ֱ������ϵ�У���Aλ��y���ϣ�����·��BC��x���ϣ���B��A�ı�ƫ��60�㷽���ϣ���C�ڵ�A�ı�ƫ��45�㷽���ϣ�����һ���ߵȼ���·��y���ϣ�OAΪ����һ�Σ�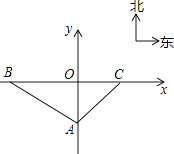
��1�����B��C�����꣮
��2��һ�������ӵ�B������ʻ����C����ʱ��Ϊ15�룮����ͨ�����㣬�жϸ��������������·���Ƿ��٣����ο����ݣ� ![]() ��
��
���𰸡�
��1��
�⣺��Rt��AOB�У�OA=100����BAO=60�㣬
��OB=OAtan��BAO=100 ![]() ��
��
Rt��AOC��
�ߡ�CAO=45�㣬
��OC=OA=100��
��B����100 ![]() ��0����C��100��0��
��0����C��100��0��
��2��
�⣺��BC=BO+OC=100 ![]() +100��
+100��
�� ![]() ��18��
��18�� ![]() ��
��
���������������·�ϳ�����
����������1����֪OA=100m����B��C�����������OB��OC�ij��ȣ�����ת��Ϊ��ֱ�������Σ���2���ж��Ƿ��پ�����BC�ij���Ȼ��Ƚϣ�
�����㾫�������ڱ��⿼��Ĺ��ڷ�������⣬��Ҫ�˽�ָ����ָ�Ϸ�������Ŀ�귽�� �����ɵ�С��90���ˮƽ�ǣ���������Dz��ܵó���ȷ�𰸣�

����Ŀ����ͼ����AOB��30����������һ��P��PO��10cm�������ϸ���һ��Q��R(����ͬ�ڵ�O)������PQR���ܳ�����Сֵ�Ƕ��٣�