题目内容
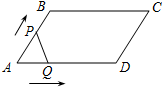
如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm
2),则y与x的函数图象大致是( )
分析:当点P在AB上时,易得S△APQ的关系式;当点P在BC上时,高不变,但底边在增大,所以P、Q经过的路径与线段PQ围成的图形的面积关系式为一个一次函数;当P在CD上时,表示出所围成的面积关系式,根据开口方向判断出相应的图象即可.
解答:解:当点P在AB上时,即0≤x≤3时,P、Q经过的路径与线段PQ围成的图形的面积=
x×
x=
x2;
当点P在BC上时,即3≤x≤9时,P、Q经过的路径与线段PQ围成的图形的面积=
×3×
3+
(2x-6+x-3)
3=
x-
,y随x的增大而增大;
当点P在CD上时,即9≤x≤12时,P、Q经过的路径与线段PQ围成的图形的面积=12×
3-
(12-x)(-
x+12
)=
-x2+12
x-36
;
综上,图象A符合题意.
故选A.
点评:本题主要考查了动点问题的函数图象,考查了学生从图象中读取信息的能力,正确列出表达式,是解答本题的关键.
练习册系列答案
相关题目
 如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
如图,在平行四边形ABCD中,∠A=60°,AB=6厘米,BC=12厘米,点P、Q同时从 顶点A出发,点P沿A→B→C→D方向以2厘米/秒的速度前进,点Q沿A→D方向以1厘米/秒的速度前进,当Q到达点D时,两个点随之停止运动.设运动时间为x秒,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x的函数图象大致是( )
 同步练习强化拓展系列答案
同步练习强化拓展系列答案 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为