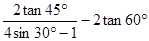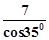题目内容
(本小题满分10分)
在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:

第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2)
请解答以下问题:
小题1:(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论.
小题2:(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?
在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:

第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2)
请解答以下问题:
小题1:(1)如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论.
小题2:(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?
小题1:(1)△BMP是等边三角形.
证明:连结AN ∵EF垂直平分AB ∴AN = BN
由折叠知AB = BN
∴AN = AB = BN ∴△ABN为等边三角形
∴∠ABN =60° ∴∠PBN =30°
又∵∠ABM =∠NBM =30°,∠BNM =∠A =90°
∴∠BPN =60°∠MBP =∠MBN +∠PBN =60°
∴∠BMP =60°
∴∠MBP =∠BMP =∠BPM =60°
∴△BMP为等边三角形 .

小题2:(2)要在矩形纸片ABCD上剪出等边△BMP,则BC≥BP
在Rt△BNP中,BN = BA =a,∠PBN =30°
∴BP =
 ∴b≥
∴b≥ ∴a≤
∴a≤ b .
b .∴当a≤
 b时,在矩形上能剪出这样的等边△BMP
b时,在矩形上能剪出这样的等边△BMP略

练习册系列答案
相关题目




 ﹥300时,则
﹥300时,则 的值
的值 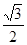 。(填“>”“<”“=”)
。(填“>”“<”“=”)

 -
-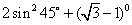
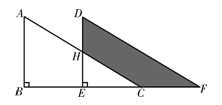
 方向平移得到
方向平移得到 .如果
.如果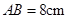 ,
,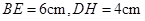 ,则图中阴影部分面积为
,则图中阴影部分面积为 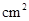 .
.