题目内容
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);
(2)M点坐标为(2,﹣3)或(1+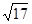 ,3)或(1﹣
,3)或(1﹣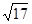 ,3);
,3);
(3)结论:在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).
解析试题分析:(1)令Y=0,X=0就可以得到
根据已知先求得对称轴,由于△MAD的面积与△CAD的面积相等,所以有两种情况,一种是点M在X轴下方,此时点M与点C关于对称轴对称,另一种是点M在X轴上方,由于面积相等,而AD是两个三角形公用的,所以可知点M的纵坐标为3,将Y=3代入解析式就可求得.
分情况讨论,一种是BC、AP为底,此时P点与D点重合;一种是AB、CP为底,此时要先求出AB所在直线的解析式,然后根据互相平行的两直线的K值相等,求出CP的解析式,与二次函数的解析式联立,得到方程组,求解即可得到。
试题解析:(1)∵y=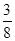 x2﹣
x2﹣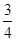 x﹣3,∴当y=0时,
x﹣3,∴当y=0时,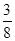 x2﹣
x2﹣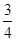 x﹣3=0,
x﹣3=0,
解得x1=﹣2,x2=4.当x=0,y=﹣3.
∴A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);
(2)∵y=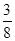 x2﹣
x2﹣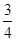 x﹣3,∴对称轴为直线x=
x﹣3,∴对称轴为直线x=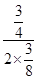 =1.
=1.
∵AD在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,﹣3),∴M点坐标为(2,﹣3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.当y=3时,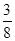 x2﹣
x2﹣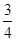 x﹣3=3,解得x1=1+
x﹣3=3,解得x1=1+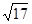 ,x2=1﹣
,x2=1﹣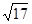 ,
,
∴M点坐标为(1+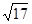 ,3)或(1﹣
,3)或(1﹣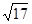 ,3).
,3).
综上所述,所求M点坐标为(2,﹣3)或(1+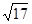 ,3)或(1﹣
,3)或(1﹣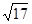 ,3);
,3);
(3)结论:存在.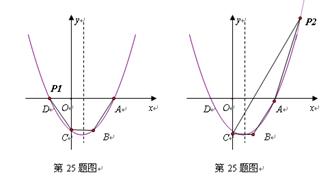
如图所示,在抛物线上有两个点P满足题意:
①若BC∥AP1,此时梯形为ABCP1.
由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,
∴P1(﹣2,0).∵P1A=6,BC=2,∴P1A≠BC,∴四边形ABCP1为梯形;
②若AB∥CP2,此时梯形为ABCP2.
∵A点坐标为(4,0),B点坐标为(2,﹣3),∴直线AB的解析式为y=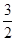 x﹣6,
x﹣6,
∴可设直线CP2的解析式为y=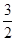 x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
∴直线CP2的解析式为y=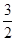 x﹣3.∵点P2在抛物线y=
x﹣3.∵点P2在抛物线y=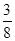 x2﹣
x2﹣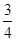 x﹣3上,
x﹣3上,
∴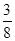 x2﹣
x2﹣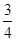 x﹣3=
x﹣3=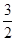 x﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
x﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,∴P2(6,6).
∵AB∥CP2,AB≠CP2,∴四边形ABCP2为梯形.
综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).
考点:1、二次函数的性质;2、等积三角形;3、梯形;4、解方程

 阅读快车系列答案
阅读快车系列答案 的根是
的根是 和
和 .
. ,则CD=3.
,则CD=3. 的图象上,则k=﹣1.
的图象上,则k=﹣1. 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与
 ,
,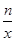 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;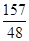 ,试求出t的取值范围.
,试求出t的取值范围.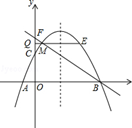
 x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ; (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;

 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
. ,求点F的坐标;
,求点F的坐标;
