Question

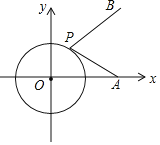
【题目】如图，斜坡AB长10米，按图中的直角坐标系可用表示，点A，B分别在x轴和y轴上，且．在坡上的A处有喷灌设备，喷出的水柱呈抛物线形落到B处，抛物线可用表示．

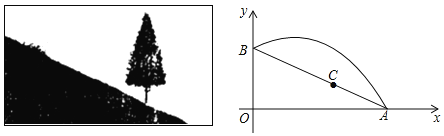
（1）求抛物线的函数关系式（不必写自变量取值范围）；

（2）求水柱离坡面AB的最大高度；

（3）在斜坡上距离A点2米的C处有一颗3.5米高的树，水柱能否越过这棵树？

Answer 1

【答案】（1）；（2）米；（3）水柱能越过树

【解析】

（1）根据直角三角形的性质求出点A、B的坐标，再利用待定系数法求解可得；

（2）水柱离坡面的距离d=-x2+x+5-（-x+5），整理成一般式，再配方成顶点式即可得；

（3）先求出点C的坐标为（4，1），再求出x=4时的函数值y，与1+3.5比较大小即可得．

（1）∵AB=10、∠OAB=30°，

∴OB=AB=5、OA=ABcos∠OAB=10×=5，

则A（5，0）、B（0，5），

将A、B坐标代入y=-x2+bx+c，得：

，

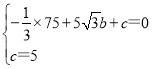解得：，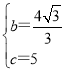

∴抛物线解析式为y=-x2+x+5；

（2）水柱离坡面的距离d=-x2+x+5-（-x+5）

=-x2+x

=-（x2-5x）

=-（x-）2+，

∴当x=时，水柱离坡面的距离最大，最大距离为米；

（3）如图，过点C作CD⊥OA于点D，

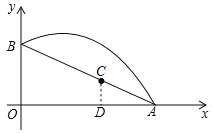
∵AC=2、∠OAB=30°，

∴CD=1、AD=，

则OD=4，

当x=4时，y=-×（4）2+×4+5=5＞1+3.5，

所以水柱能越过树．