题目内容
【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°. 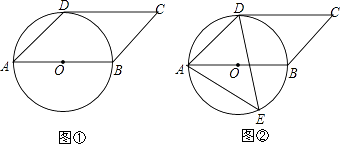
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
【答案】
(1)解:(1)CD与圆O相切.
证明:如图①,连接OD,
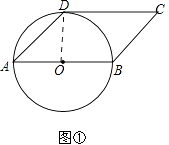
则∠AOD=2∠DAB=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD.
∴CD与圆O相切.
(2)如图②,作EF⊥AB于F,连接BE,
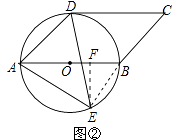
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6.
∵AE=5,
∴BE= ![]() =
= ![]() ,
,
∵sin∠BAE= ![]() .
.
∴ ![]() =
= ![]()
∴EF= ![]() .
.
【解析】(1)连接OD,则∠AOD为直角,由四边形ABCD是平行四边形,则AB∥DC.从而得出∠CDO=90°,即可证出答案.(2)作EF⊥AB于F,连接BE,根据圆周角定理得∠AEB=90°,然后根据勾股定理求得BE,然后根据sin∠BAE= ![]() 求得EF即可.
求得EF即可.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.

练习册系列答案
相关题目
【题目】某公司要将一批货物运往某地,打算租用某汽车运输公司的甲.乙两种货车,以前租用这两种货车的信息如下表所示;
第一次 | 第二次 | |
甲种货车辆数/辆 | 2 | 5 |
乙种货车辆数/辆 | 3 | 6 |
累计运货量/吨 | 15.5 | 35 |
现打算租用该公司4辆甲种货车和6辆乙种货车,可一次刚好运完这批货物.如果每吨运费为50元,该公司应付运费________元.