题目内容
如图,菱形ABCD的边长为6,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△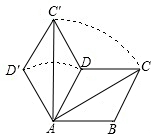 AC′D′,连接DC′.
AC′D′,连接DC′.(1)求证:△ADC≌△ADC′.
(2)求在旋转过程中线段CD扫过图形的面积.(结果保留π).
分析:(1)利用旋转的不变性可以得到相等的线段和相等的角,从而为证明全等提供必要的条件;
(2)计算旋转的角度可以得到旋转角,代入扇形面积公式计算即可.
(2)计算旋转的角度可以得到旋转角,代入扇形面积公式计算即可.
解答:解:(1)由旋转可知:AC=AC′,∠CAC′=60°.
在菱形ABCD中,∠BAD=60°
∴∠DAC=
∠DAB=30°,
∴∠DAC=∠DAC′.
又∵AC=AC′,AD=AD
∴△ADC≌△ADC′;
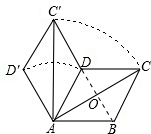
(2)连接BD交AC于点O,
则BD⊥AC,AC=2AO.
在Rt△AOD中,∠DAO=30°,AD=6,
∴AO=3
.
∴AC=2AO=6
∴S扇形ACC′=
=18π.
∵S扇形ADD′=
=6π,
∴CD扫过图形的面积为18π-6π=12π.
在菱形ABCD中,∠BAD=60°
∴∠DAC=
| 1 |
| 2 |
∴∠DAC=∠DAC′.
又∵AC=AC′,AD=AD
∴△ADC≌△ADC′;

(2)连接BD交AC于点O,
则BD⊥AC,AC=2AO.
在Rt△AOD中,∠DAO=30°,AD=6,
∴AO=3
| 3 |
∴AC=2AO=6
| 3 |
∴S扇形ACC′=
60×π×(6
| ||
| 360 |
∵S扇形ADD′=
| 60×π×62 |
| 360 |
∴CD扫过图形的面积为18π-6π=12π.
点评:本题考查了全等三角形的判定、旋转的性质、菱形的性质等知识,解题的关键是牢记旋转不变量.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
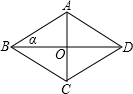 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
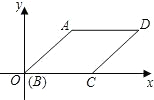 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.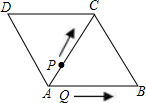 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).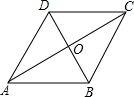 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.