题目内容
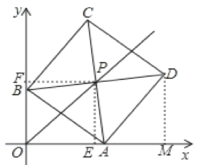
【题目】在平面直角坐标系xOy中,边长为5的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C. D都在第一象限。
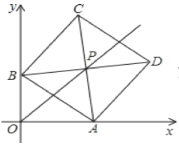
(1)当点A坐标为(4,0)时,求点D的坐标;
(2)求证:OP平分∠AOB;
(3)直接写出OP长的取值范围(不要证明).
【答案】(1)D(7,4);(2)见解析;(3)![]() <OP5.
<OP5.
【解析】
(1)作DM⊥x轴于点M,由A(4,0)可以得出OA=4,由勾股定理就可以求出OB=3,再通过证明△AOB≌△DMA就可以求出AM=OB,DM=OA,从而求出点D的坐标.
(2)过P点作x轴和y轴的垂线,可通过三角形全等,证明OP是角平分线.
(3)因为OP在∠AOB的平分线上,就有∠POA=45°,就有OP=![]() PE,在Rt△APE中运用三角函数就可以表示出PE的范围,从而可以求出OP的取值范围.
PE,在Rt△APE中运用三角函数就可以表示出PE的范围,从而可以求出OP的取值范围.
(1)作DM⊥x轴于点M,
∴∠AMD=90°.
∵∠AOB=90°,
∴∠AMD=∠AOB.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠OAB+∠DAM=90.
∵∠OAB+∠OBA=90°,
∴∠DAM=∠OBA.
在△DMA和△AOB中,
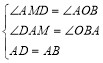 ,
,
∴△DMA≌△AOB,
∴AM=OB,DM=AO.
∵A(4,0),
∴OA=4,
∵AB=5,在Rt△AOB中由勾股定理得:
OB=![]() =3.
=3.
∴AM=3,MD=4,
∴OM=7.
∴D(7,4);
(2)证明:作PE⊥x轴交x轴于E点,作PF⊥y轴交y轴于F点
∵∠BPE+∠EPA=90°,∠EPB+∠FPB=90°,
∴∠FPB=∠EPA,
∵∠PFB=∠PEA,BP=AP,
∴△PBF≌△PAE,
∴PE=PF,
∴点P都在∠AOB的平分线上.
(3)作PE⊥x轴交x轴于E点,作PF⊥y轴交y轴于F点,则PE=h,设∠APE=α.
在直角△APE中,∠AEP=90°,PA=![]() .
.
∴PE=PAcosα=![]() cosα.
cosα.
∵顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),
∴0°α<45°,
∴![]() <cosα1.
<cosα1.
∴![]() <PE
<PE![]() ,
,
∵OP=![]() PE,
PE,
∴![]() <OP5.
<OP5.

 寒假学与练系列答案
寒假学与练系列答案【题目】仙居吾悦广场于![]() 年
年![]() 月
月![]() 日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
购买服装总金额(元) | 不超过 | 超过 |
|
优惠幅度 | 打 | 打 | 打 |
乙服装店优惠活动:购买服装总金额每满![]() 元减
元减![]() 元.
元.
例如:购买总金额满![]() 元减
元减![]() 元,满
元,满![]() 元减
元减![]() 元,以此类推.
元,以此类推.
(1)若在两家店购买服装总金额都是![]() 元,哪家店实际付款更少?少多少?
元,哪家店实际付款更少?少多少?
(2)若购买服装总金额小于![]() 元,选择哪家店购买服装更划算?请通过计算说明理由.
元,选择哪家店购买服装更划算?请通过计算说明理由.