Question

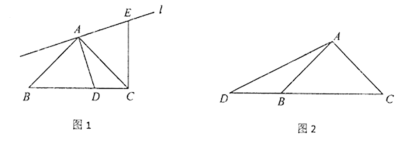
【题目】在平面直角坐标系中，点A（0，5），B（12，0），在y轴负半轴上取点E，使OA＝EO，作∠CEF＝∠AEB，直线CO交BA的延长线于点D．

（1）根据题意，可求得OE＝　 　；

（2）求证：△ADO≌△ECO；

（3）动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位，到B点处停止运动；动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位，到E点处停止运动．二者同时开始运动，都要到达相应的终点才能停止．在某时刻，作PM⊥CD于点M，QN⊥CD于点N．问两动点运动多长时间△OPM与△OQN全等？

Answer 1

【答案】（1）5；（2）见解析；（3）当两动点运动时间为、、10秒时，△OPM与△OQN全等

【解析】

（1）根据OA=OE即可解决问题．
（2）根据ASA证明三角形全等即可解决问题．
（2）设运动的时间为t秒，分三种情况讨论：当点P、Q分别在y轴、x轴上时；当点P、Q都在y轴上时；当点P在x轴上，Q在y轴时若二者都没有提前停止，当点Q提前停止时；列方程即可得到结论．

（1）∵A（0，5），

∴OE＝OA＝5，

故答案为5．

（2）如图1中，

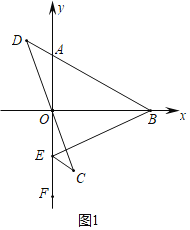
∵OE＝OA，OB⊥AE，

∴BA＝BE，

∴∠BAO＝∠BEO，

∵∠CEF＝∠AEB，

∴∠CEF＝∠BAO，

∴∠CEO＝∠DAO，

在△ADO与△ECO中，

，

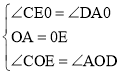∴△ADO≌△ECO（ASA）．

（2）设运动的时间为t秒，当PO＝QO时，易证△OPM≌△OQN．

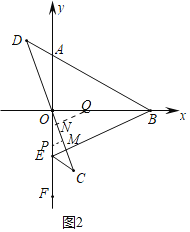
分三种情况讨论：

①当点P、Q分别在y轴、x轴上时PO＝QO得：

5﹣t＝12﹣3t，

解得t＝（秒），

②当点P、Q都在y轴上时PO＝QO得：

5﹣t＝3t﹣12，

解得t＝（秒），

③当点P在x轴上，Q在y轴上时，

若二者都没有提前停止，则PO＝QO得：

t﹣5＝3t﹣12，

解得t＝（秒）不合题意；

当点Q运动到点E提前停止时，

有t﹣5＝5，解得t＝10（秒），

综上所述：当两动点运动时间为、、10秒时，△OPM与△OQN全等．