题目内容
【题目】如图,已知线段AB,根据以下作图过程:
(1)分别以点A、点B为圆心,大于AB长的![]() 为半径作弧,两弧相交于C、D两点;
为半径作弧,两弧相交于C、D两点;
(2)过C、D两点作直线CD.
求证:直线CD是线段AB的垂直平分线.

【答案】见解析
【解析】
连接AC、BC、AD、BD,根据SSS证明△ACD≌BCD,从而得到∠ACO=∠BCO、∠ADO=∠BDO,再根据SAS证明△AOC≌BOC,△AOD≌△BOD,从而得到AO=BO,OC⊥AB,OC⊥AB,再得出结论.
连接AC、BC、AD、BD,如图所示:

∵分别以点A、点B为圆心,大于AB长的![]() 为半径作弧,两弧相交于C、D两点,
为半径作弧,两弧相交于C、D两点,
∴AC=BC,AD=BD,
在△ACD和△BCD中
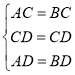 ,
,
∴△ACD≌△BCD,
∴∠ACO=∠BCO、∠ADO=∠BDO,
在△AOC和△BOC中,
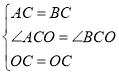 ,
,
∴△AOC≌BOC,
∴OA=OB,∠COA=∠COB=90,
∴OC垂直平分AB,
同理可证△AOD≌△BOD,OC垂直平分AB,
∴直线CD是线段AB的垂直平分线.

 阅读快车系列答案
阅读快车系列答案【题目】数学课上,李老师出示了如下框中的题目.
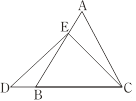
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).
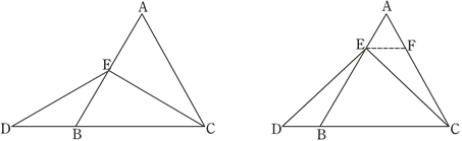
图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
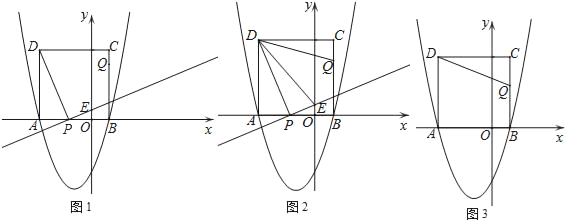
【题目】如图,平面直角坐标系中直线![]() :
:![]() 分别与x轴,y轴交于点A和点B,过点A的直线
分别与x轴,y轴交于点A和点B,过点A的直线![]() 与y轴交于点C,
与y轴交于点C,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)若D为线段![]() 上一点,E为线段
上一点,E为线段![]() 上一点,当
上一点,当![]() 时,求
时,求![]() 的最小值,并求出此时点E的坐标.
的最小值,并求出此时点E的坐标.
【题目】某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,开展了一次调查研究,请将下面的过程补全.
收集数据:
(1)调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);
A.抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本
B.抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本
C.从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本
整理、描述数据:
抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:
77 83 80 64 86 90 75 92 83 81
85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82
91 81 86 71 53 72 90 76 68 78
整理数据,如下表所示:
2018年九年级部分学生学生的体质健康测试成绩统计表
|
|
|
|
|
|
|
|
|
|
1 | 1 | 2 | 2 | 4 | 5 | 5 | 2 |
分析数据、得出结论
调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,

(2)你能从中得到的结论是_____________,你的理由是________________________________.
(3)体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有________名同学参加此项目.