题目内容
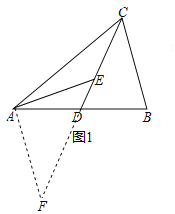
【题目】如图1,△ABC中,CD为△ABC的中线,点E在CD上,且∠AED=∠BCD.

(1)求证:AE=BC.
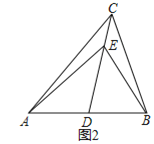
(2)如图2,连接BE,若AB=AC=2DE,∠CBE=14°,则∠ACD的度数为 (直接写出结果),
【答案】(1)详见解析;(2)28°.
【解析】
(1)延长CD到F使DF=CD,连接AF,由CD是△ABC的中线,得到AD=BD,推出△ADF≌△BCD,根据全等三角形的性质得到∠F=∠BCD,BC=AF,由等腰三角形的性质,利用等量代换即可得到结论;
(2)根据DE=![]() AB,CD为△ABC的中线,得DE=AD=DB,∠DEB=∠DBE,可求得∠ABC=∠DEB+14°,并∠DEB=∠DCB+∠CBE,的∠DCB=∠DEB﹣14°,利用AC=AB,得∠ACB=∠ABC=∠DEB+14°,即可得∠ACD=∠ACB﹣∠DCB=28°.
AB,CD为△ABC的中线,得DE=AD=DB,∠DEB=∠DBE,可求得∠ABC=∠DEB+14°,并∠DEB=∠DCB+∠CBE,的∠DCB=∠DEB﹣14°,利用AC=AB,得∠ACB=∠ABC=∠DEB+14°,即可得∠ACD=∠ACB﹣∠DCB=28°.
证明:(1)如图1,延长CD到F,使DF=CD,连接AF,
∵CD为△ABC的中线,
∴AD=BD,且∠ADF=∠BDC,且CD=DF,
∴△ADF≌△BDC(SAS),
∴AF=BC,∠F=∠BCD,
∵∠AED=∠BCD,
∴∠AED=∠F,
∴AE=AF,
∴AE=BC;
(2)
∵DE=![]() AB,CD为△ABC的中线,
AB,CD为△ABC的中线,
∴DE=AD=DB,
∴∠DEB=∠DBE,
∴∠ABC=∠DBE+∠CBE=∠DEB+14°,
∵∠DEB=∠DCB+∠CBE,
∴∠DCB=∠DEB﹣14°,
∵AC=AB,
∴∠ACB=∠ABC=∠DEB+14°
∴∠ACD=∠ACB﹣∠DCB=(∠DEB+14°)-(∠DEB﹣14°)=28°,
故答案为:28°.

练习册系列答案
相关题目