题目内容
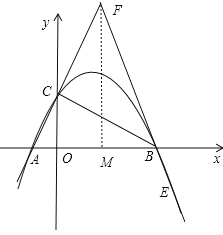
【题目】(2017广东省深圳市)如图,抛物线![]() 经过点A(﹣1,0),B(4,0),交y轴于点C;
经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使![]() ?若存在请直接给出点D坐标;若不存在,请说明理由;
?若存在请直接给出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.

【答案】(1)![]() ;(2)D坐标为(1,3)或(2,3)或(5,﹣3);(3)
;(2)D坐标为(1,3)或(2,3)或(5,﹣3);(3)![]() .
.
【解析】试题(1)由A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)由条件可求得点D到x轴的距离,即可求得D点的纵坐标,代入抛物线解析式可求得D点坐标;
(3)由条件可证得BC⊥AC,设直线AC和BE交于点F,过F作FM⊥x轴于点M,则可得BF=BC,利用平行线分线段成比例可求得F点的坐标,利用待定系数法可求得直线BE解析式,联立直线BE和抛物线解析式可求得E点坐标,则可求得BE的长.
试题解析:
(1)∵抛物线![]() 经过点A(﹣1,0),B(4,0),
经过点A(﹣1,0),B(4,0),
∴![]() ,
,
解得: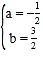 ,
,
∴抛物线解析式为![]() ;
;
(2)由题意可知C(0,2),A(﹣1,0),B(4,0),
∴AB=5,OC=2,
∴S△ABC=![]() ABOC=
ABOC=![]() ×5×2=5,
×5×2=5,
∵![]() ,
,
∴S△ABD=![]() ×5=
×5=![]() ,
,
设D(x,y),
∴![]() AB|y|=
AB|y|=![]() ×5|y|=
×5|y|=![]() ,
,
解得|y|=3,
当y=3时,由![]() =3,解得x=1或x=2,此时D点坐标为(1,3)或(2,3);
=3,解得x=1或x=2,此时D点坐标为(1,3)或(2,3);
当y=﹣3时,由![]() =﹣3,解得x=﹣2(舍去)或x=5,此时D点坐标为(5,﹣3);
=﹣3,解得x=﹣2(舍去)或x=5,此时D点坐标为(5,﹣3);
综上可知存在满足条件的点D,其坐标为(1,3)或(2,3)或(5,﹣3);
(3)∵AO=1,OC=2,OB=4,AB=5,
∴AC=![]() =
=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,即BC⊥AC,
如图,设直线AC与直线BE交于点F,过F作FM⊥x轴于点M,由题意可知∠FBC=45°,∴∠CFB=45°,
∴CF=BC=![]() ,
,
∴![]() ,即
,即![]() ,解得OM=2,
,解得OM=2,
![]() ,即
,即![]() ,解得FM=6,
,解得FM=6,
∴F(2,6),且B(4,0),
设直线BE解析式为y=kx+m,则可得:![]() ,解得:
,解得:![]() ,
,
∴直线BE解析式为y=﹣3x+12,
联立直线BE和抛物线解析式可得: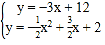 ,
,
解得:![]() 或
或![]() ,
,
∴E(5,﹣3),
∴BE=![]() =
=![]() .
.